選択した画像 円周角の定��の逆 証明 205328-円周角の��理の逆 証明 転換法
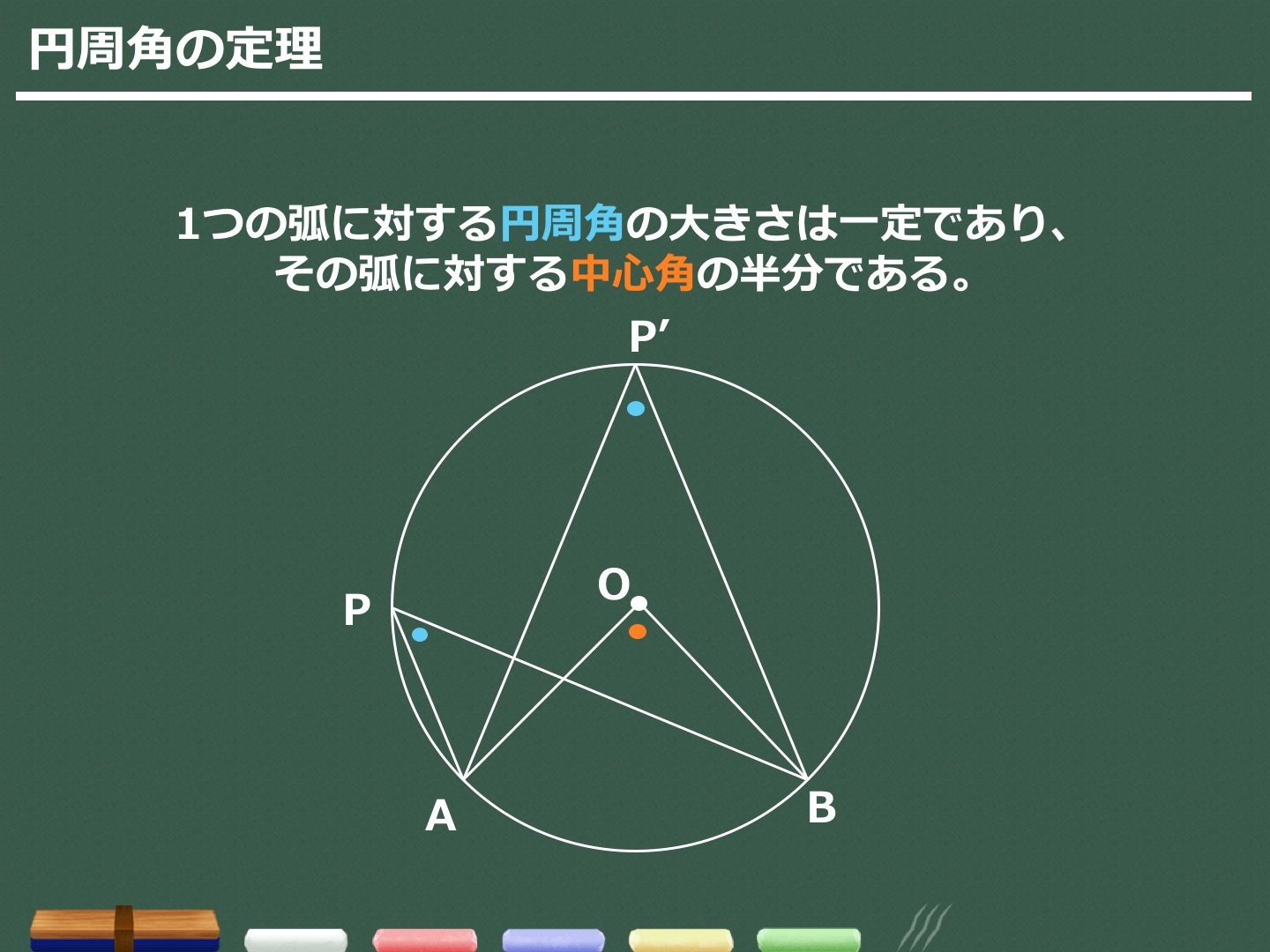
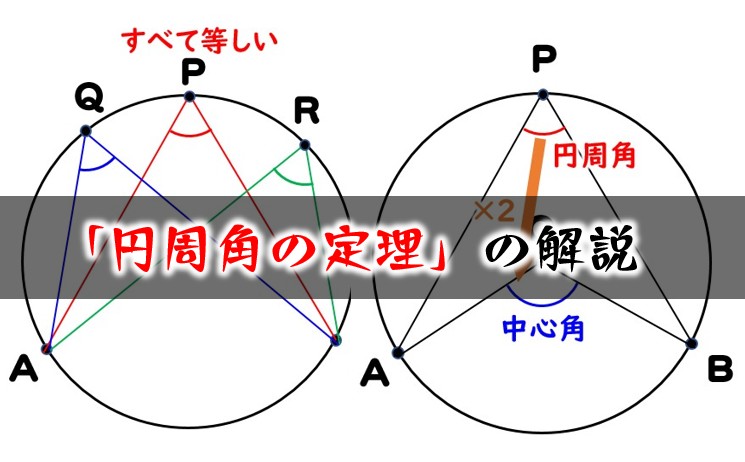
証明の流れ 1.「(円周角) $=\dfrac12\times$(中心角)」を示す. → 円の中心Oがどの位置にあるかで3通りに場合分け.2 円周角の定理を証明しよう 21 22 中心Oが円周角を作る線分AP上にあるとき;円周角の定理 ・ 円周角の定理から派生する定理 ・ 例題問題 円周角の定理を利用して色々な角度を求めてみる ・ ここまでの各定理の証明 → 接点までの距離は等しいという証明 → 円周角の定理の証明 → 弧と円周角の定理の証明 ② 円周角の定理の逆 と

円周角の定理 作図から証明まで 中3数学 中学生 数学のノート Clearnote
円周角の定理の逆 証明 転換法
円周角の定理の逆 証明 転換法- 円周角の定理の極限 次に,接弦定理が成り立つことの感覚的な説明を紹介します。 点 c c c を円周上で限りなく a a a に近づけていくと, 円周角の定理より ∠ a c b \angle acb ∠ a cb は一定 直線 c a ca c a は円の接線に近づく 以上から接弦定理が成り立つことが納得できます。円周角の定理の逆を証明します。 「円周角の定理」の授業動画 https//youtube/1NYjN1vYHdo 図形の性質の再生リストはコチラ



3分でわかる 円周角の定理の逆の証明 Qikeru 学びを楽しくわかりやすく
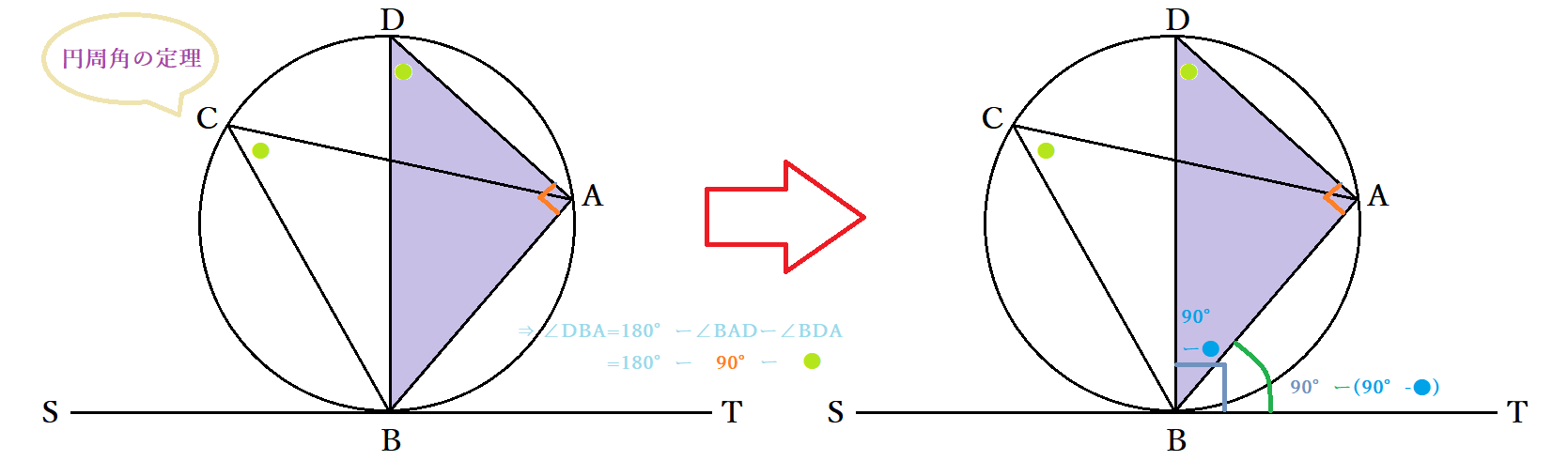
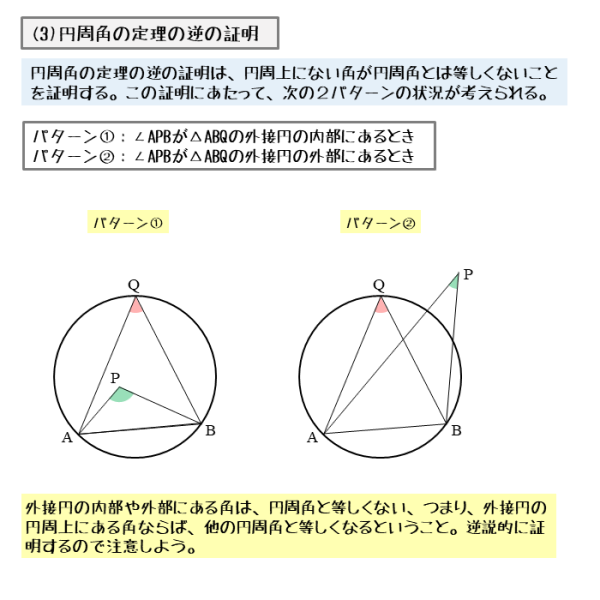
円周角と中心角(3) 等しい弧と円周角 円周角と図形の証明 円周角の定理の逆 円周角の定理の活用 7 三平方の定理 三平方の定理の証明(1) 問題一括 (3,793Kb) 解答一括 (4,569Kb) 三平方の定理の証明(2) 三平方の定理の証明(3) 三平方の定理(1) 三平方の定理(2 円周角の定理の逆の証明についてです。 「画像にある円周角の定理の逆の証明において、点dが円γの外部にある場合に、弦bc上の点mを定義している。それはなぜか。」 という課題が出ました。 これに対して以下のような答案を書きました。下図のように、対角の2つの角に対する中心角の和が360°になるので、円周角の和はその半分の180°となるからです。 また、この定理から 「円に内接する四角形において、ある頂点の外角は対角の内角と等しい」 という定理も導けます。
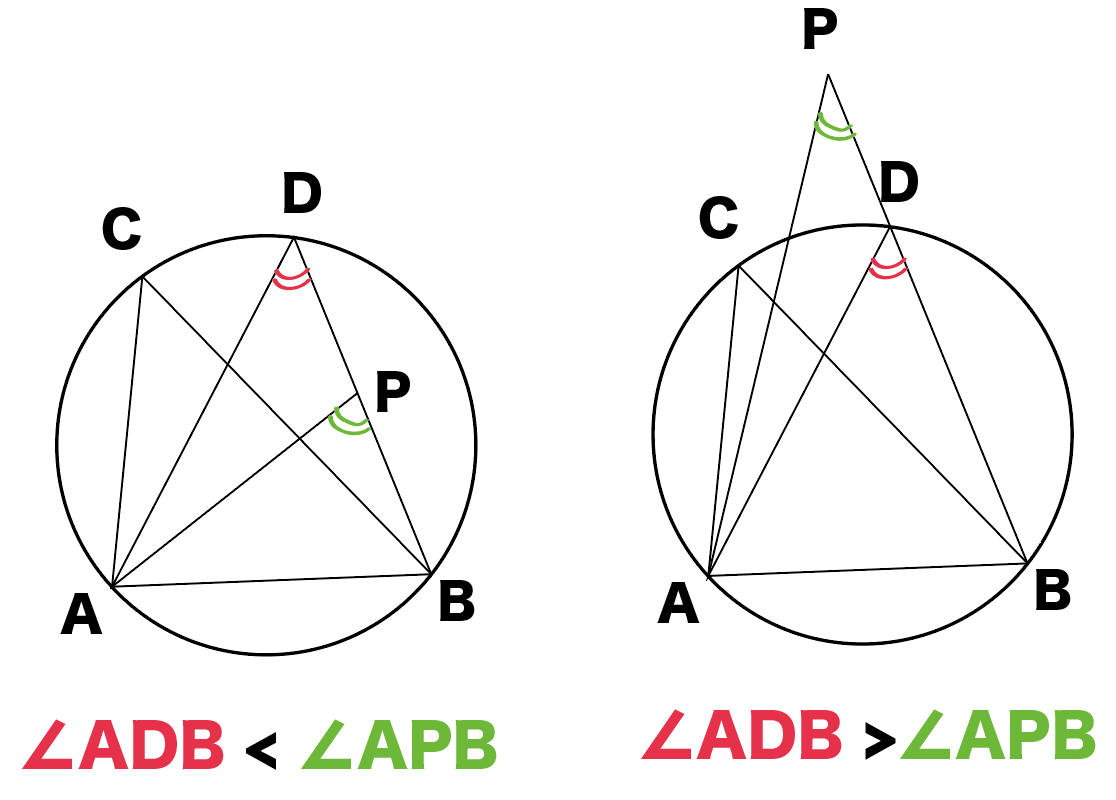
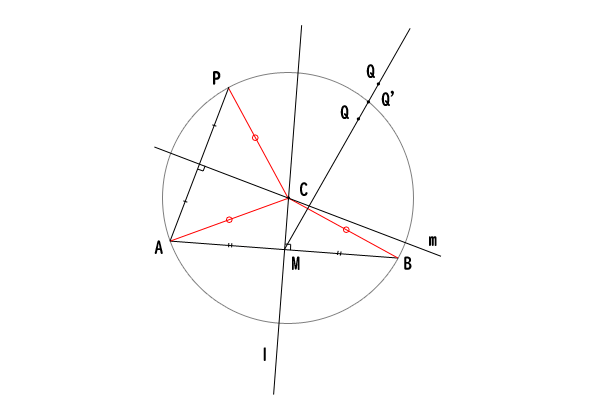
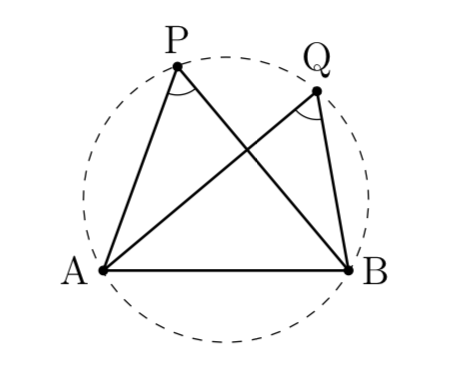
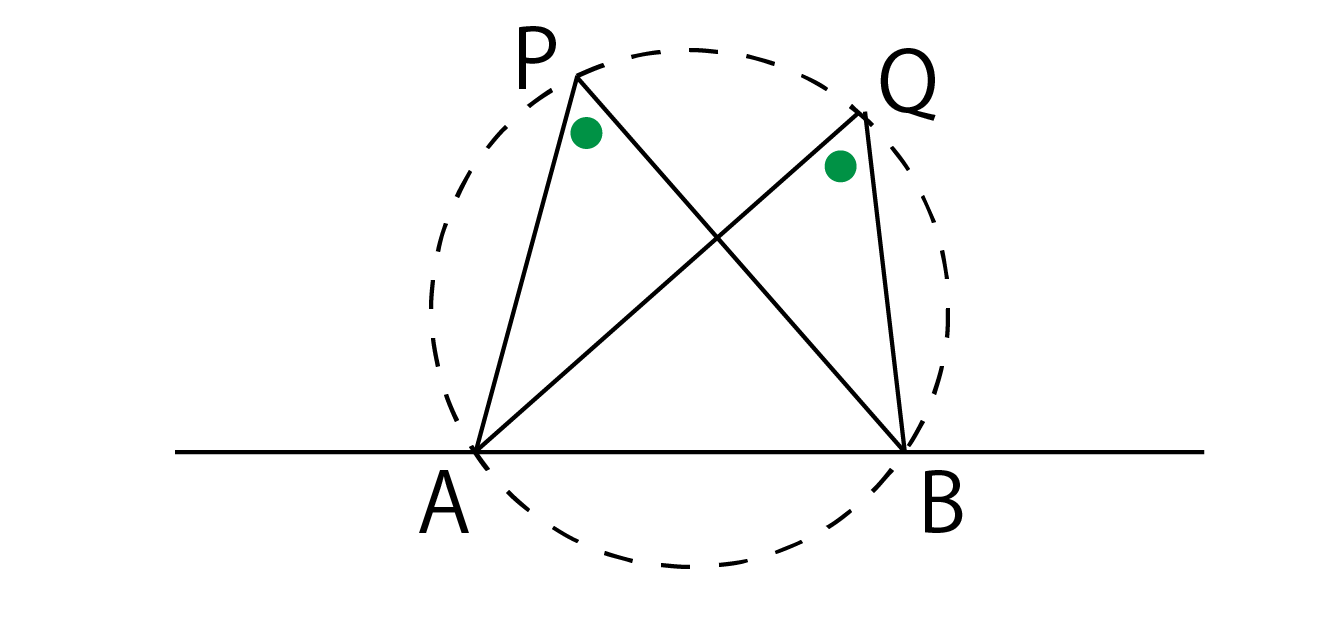
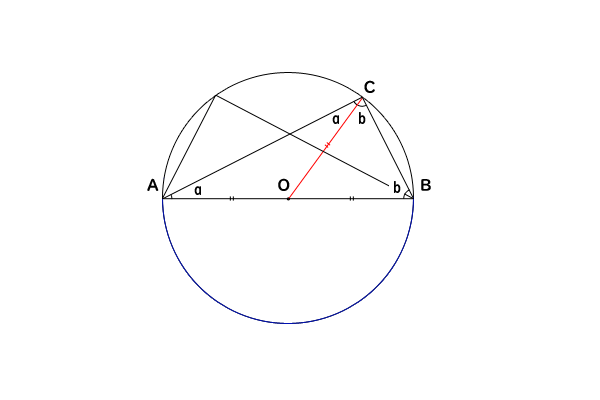
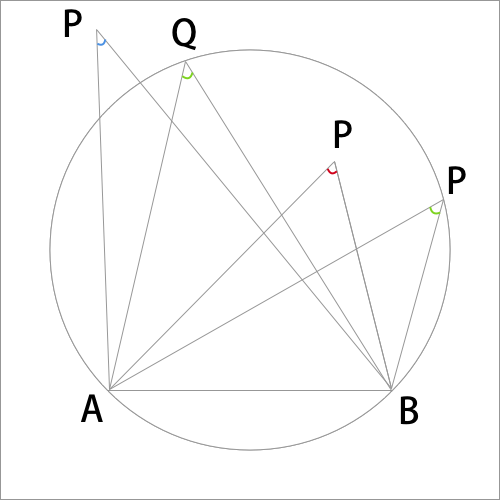
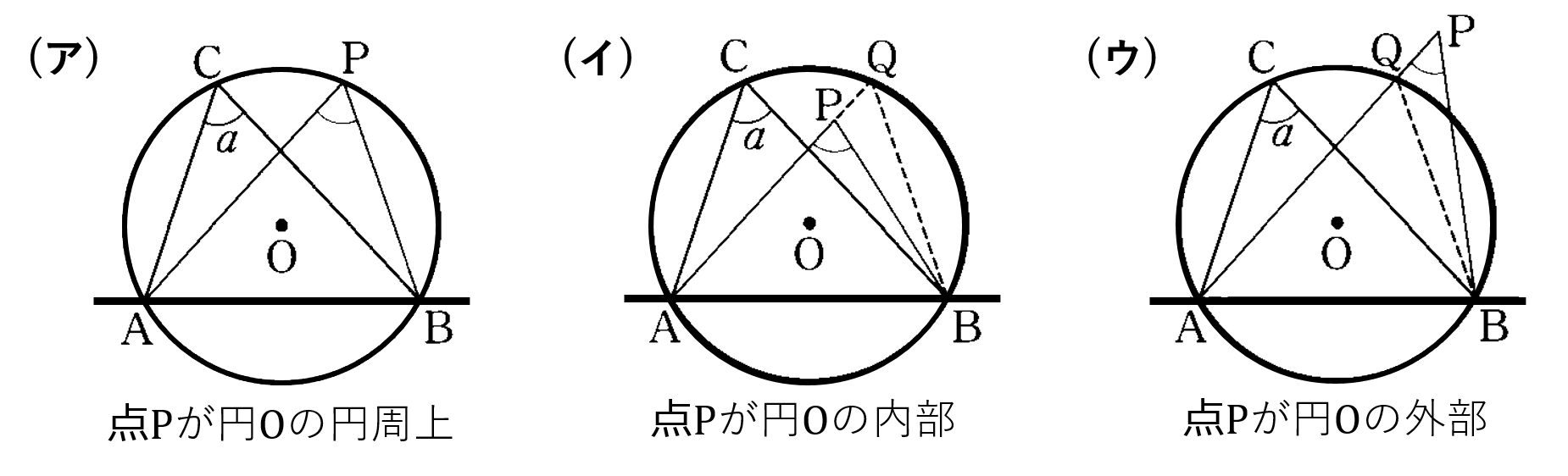
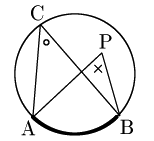
円周角の定理は,その逆の主張も成立します.これは,平面上の 4 4 点が同一周上にあるための判定法のひとつになっています. 証明は次の事実により従います. 一つの円周上に 3 3 点 A,B,C A, B, C があるとき,直線 AB A B について,点 C C と同じ側に点 P P これらの事実を持って転換法を用いると次の円周角の定理の逆が成り立つことが分かる. これをもって,いままで気になっていたことが一挙に解決した. 1)円周角の定理の証明の肝は外角定理である. 外角定理は三角形の内角の和が二直角であることを円周角の定理の逆 1つの円周上に3点a,b,qがある. 直線abに関して点qと同じ側に点pを取る. このとき ∠p=∠q →pは円周上にある この円周角の定理の逆を証明するために,円周角の定理を拡張する必
円周角の定理の逆 さて、円周角の定理の逆が正しいことを決定づけるためには、 「とある2点に対して同じ角度をとる2つの点があったとき、その点は同じ円周上にある」 ということを証明できればいい円周角の定理の証明方法について 円周角の定理は2つありますが、 「どんな場合でも円周角は常に中心角の半分である」 ということを示せば、両方の定理の証明になります。 より具体的に言えば、円周角をなす点Pの位置を動かして、3つのパターンにおい円周角の定理の系として、タレスの定理がある。 タレースの定理とは、 『三角形のうち、一辺がその外接円の直径に一致するものは直角三角形である 』 という定理である。 これは、円周角の定理から証明できる 。 脚注



3分で分かる 円周角の定理とその逆についてわかりやすく 合格サプリ




円周角の定理の逆 Youtube
2.円周角の定理の逆 先に議論した円の内部・外部の関係から,次の「円周角の定理の逆」が成り立つ: 円周角の定理の逆 2点C,Pが直線ABについて同じ側にあるとする.このとき,∠ACB = = ∠APBならば,4点A,B,C,Pは同一円周上にある.3 円周角の定理の逆を証明しよう 31 点Pが ABQの外接円の内部にあるとき;§2.円周角の定理の逆の証明 ∼単位円,ベクトルの内積,余弦定理の利用∼ 周知の通り,円周角の定理の逆とは,《円o上に異 なる3点a,b,cをとり,直線abに関してcと 同じ側に点pを∠apb=∠acb となるようにと ると,pは円o上にある。》という数学的事実で



本時のねらい 円周角と中心角の意味を理解し 二つの角の関係について 操作 実験を通して予測したことを確認し 定理としてまとめる Ppt Download




ねこ騙し数学
円周角の定理の逆とは? 次に、「円周角の定理の逆」について説明します。 逆って何?と思った方もいるでしょう。「円周角の定理の逆」とは、 図で表すと、以下のときは、 a,b,p,qが円周上にある、ということです。 なぜこうなるのか説明する前に、∠bacが ・鋭角のとき ・90°のとき ・鈍角のとき の3つの場合について証明します。 ∠bacが鋭角のとき 接点cと円の中心を通る線分ceを引く。 また、ebを結ぶ。このとき∠ebc=90° 円周角の定理より、∠cab=∠ceb 円周角の定理を使った証明の定期テスト過去問分析問題 問1 図のように、円oの円周上に5点a,b,c,d,eがある。 be//cdで、be上にfとgがある。このとき、 abg∽ edgであることを証明せ




ファイル 円周角10 Jpg Wikibooks




3分でわかる 円周角の定理の逆の証明 Qikeru 学びを楽しくわかりやすく
それを全ての頂点で数え上げると対角線はn(n3)本あるが、それぞれ2回ずつ数えているので、実際は 本である。 円周角の定理 (画像は 円周角の定理の証明 から引用) 円Oの弧ABと、円周のうちAB以外の上にある点Pをとる。面を掘ったときにできる穴の形を推測するプリント、もう1枚は「円周角の定理 の逆」の証明の補助プリントである。 数学Aプリント ① ショベルカーで地面の点Aと点Bの間に穴を掘る。最大限に土を掘り出したら、どのよ 円周角の定理の逆の問題です。 円周角の定理の逆とは 下の図で2点p,qが直線abと同じ側にあるとき、 ∠apb=∠aqbならば、 4点a, p ,q, bは1つの円周上にある。 角度から点や四角形が円周上にあるかや証明問題に使われます。 練習問題をダウンロードする



2



フェルマー点の証明 Geogebra
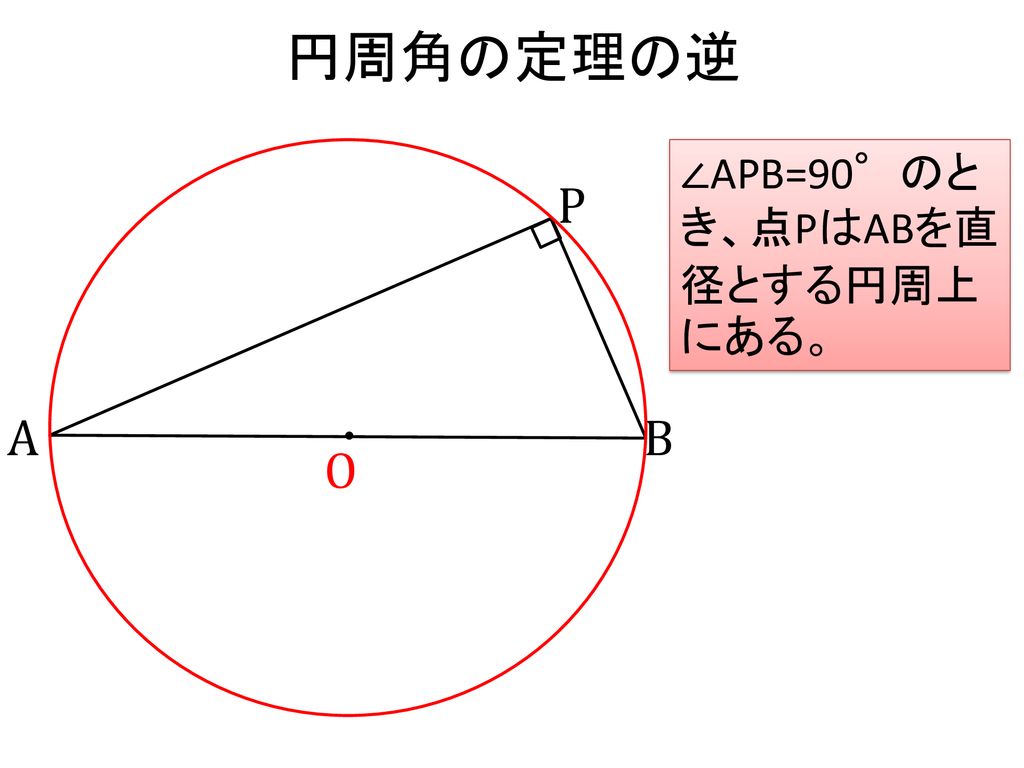
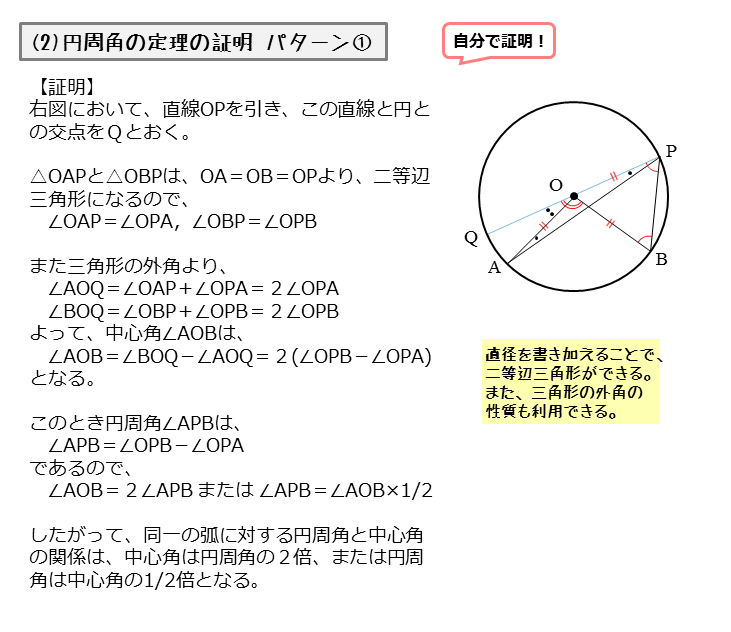
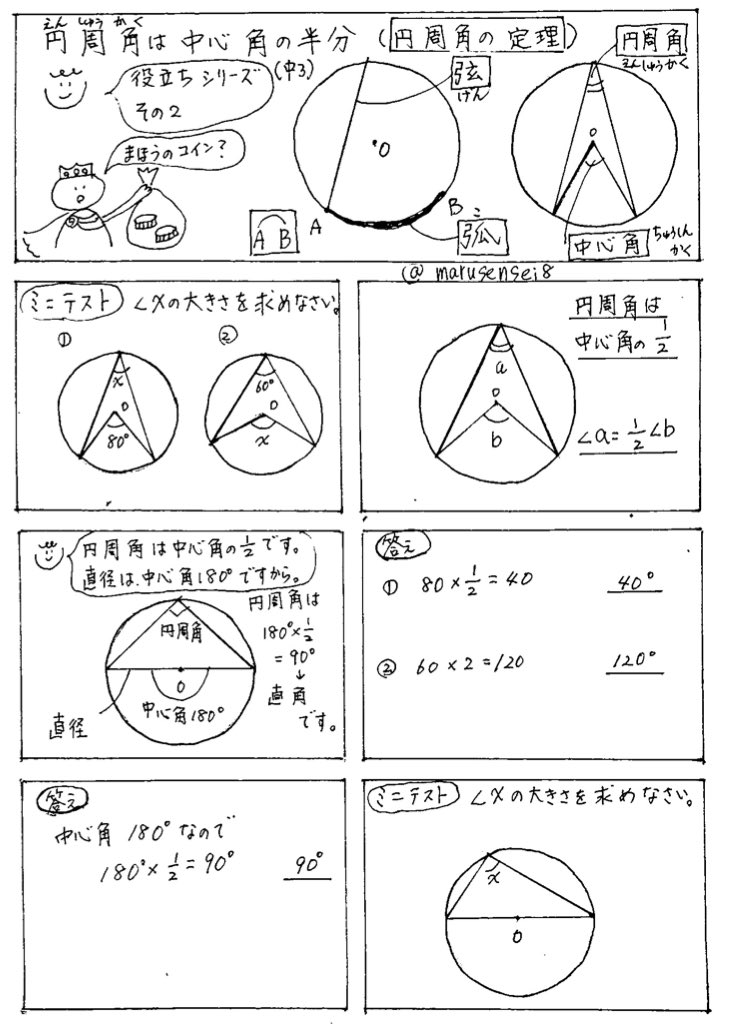
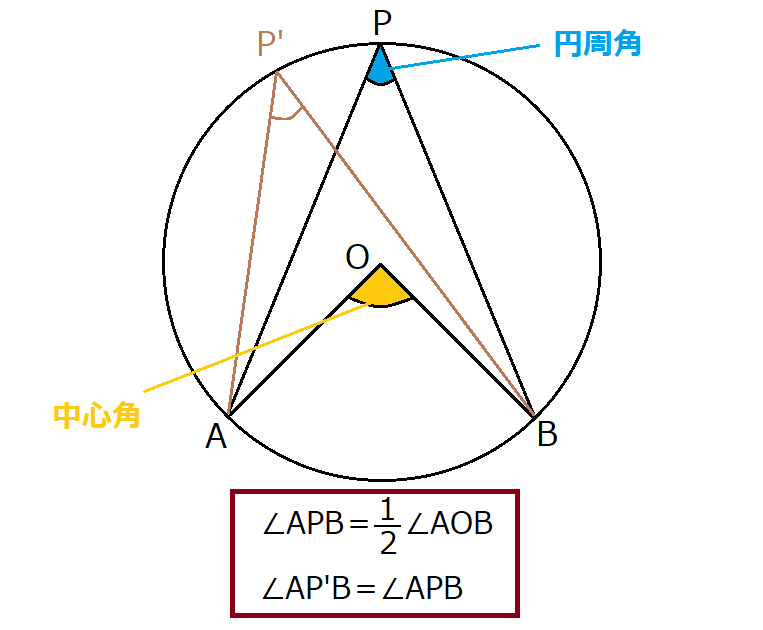
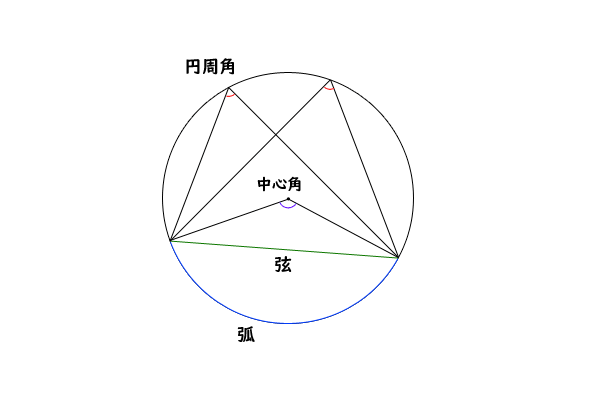
一つの弧に対する「円周角」の大きさは,「中心角」の半分になります. OC=OB= (半径)だから OBCは二等辺三角形になる. 二等辺三角形の2つの底角は等しいから ∠ B=∠ C (1) ∠ BOA=∠ B∠ C (2) 差で示します. 中心角92°が書いてあって,円周角がこの「半円の弧 A B に対する円周角 ∠ A P B は直角になる」という性質は タレスの定理 と言って、工学・建築学の世界ではよく使う性質なので、ぜひ覚えておいてください。 タレスの定理 線分 A B を直径とする円の円周上に A, B と異なる点 P をとると 円周角の定理の証明には ① 「円周角 ∠ A P B の内側」に円の中心 O がある ② 「円周角 ∠ A P B の線分上」に円の中心 O がある ③ 「円周角 ∠ A P B の外側」に円の中心 O がある の3つのパターンの証明が必要です。 このページでは、円周角の定理の証明



円周角の定理の逆とは わかりやすく解説 証明問題付き テラコヤプラス By Ameba



図形の性質 円周角について 日々是鍛錬 ひびこれたんれん
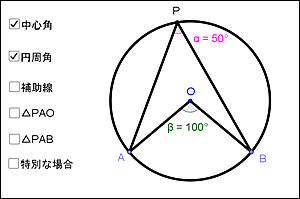



授業実践記録 数学 第3学年 数学的な見方 考え方を養う 円周角の定理 の授業 動的幾何学ソフトウェア Geogebra を用いて知識を拡張 統合する 啓林館



円周角の定理の逆



円周角の定理 Twitter Search Twitter
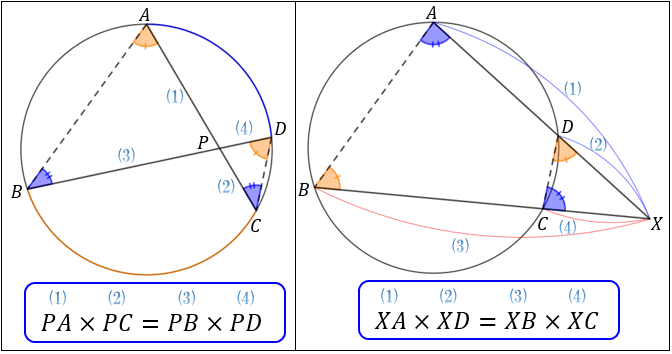



方べきの定理とは 3つのパターンの図解とその証明方法 アタリマエ




中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生



円周角の問題です これは 円周角の定理の逆を使って 点fを中心と Yahoo 知恵袋



円周角の定理とその逆 思考力を鍛える数学
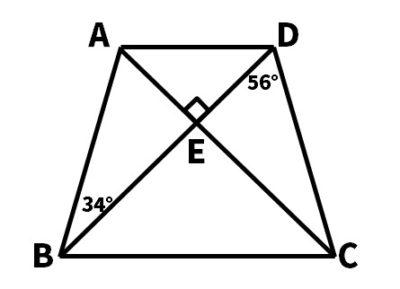



中3数学 円周角の定理の逆の定期テスト過去問分析問題 ダイスト
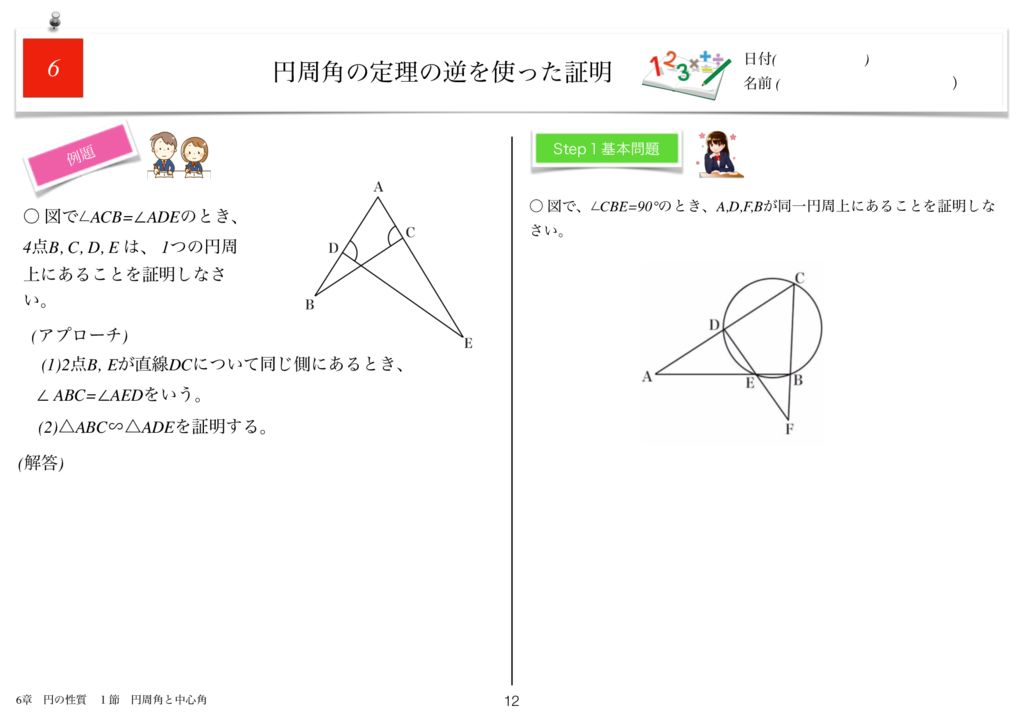



世界一わかりやすい数学問題集中3 6章 円の性質




円周角の定理 数学a フリー教材開発コミュニティ Ftext



円周角の定理とは 円周角の定理の証明や問題の解き方を完全解説 Studyplus スタディプラス




円周角の定理 中学校学習指導要領および教科書の扱い 身勝手な主張




平面図形23 円周角の定理の逆 怜悧玲瓏 高校数学を天空から俯瞰する




中3数学 円周角の定理の逆 の重要ポイント 映像授業のtry It トライイット



中3数学 パターン確認 円周角と相似 個別指導塾のyou 学舎日記 公式ブログ
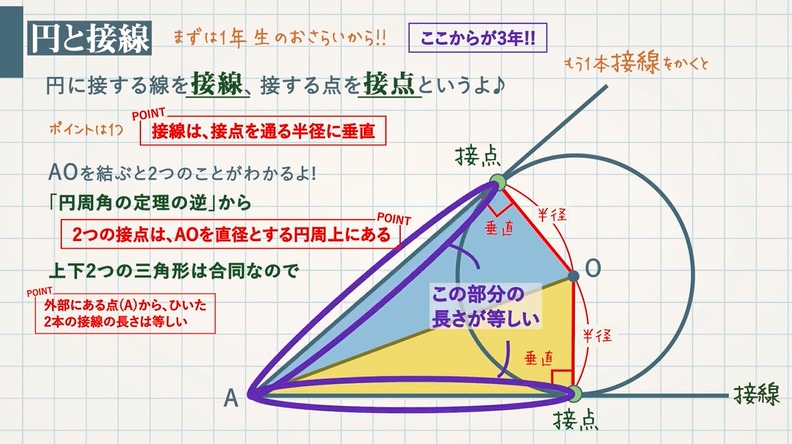



円と接線 教遊者




接線と弦の作る角 接弦定理 無料で使える中学学習プリント
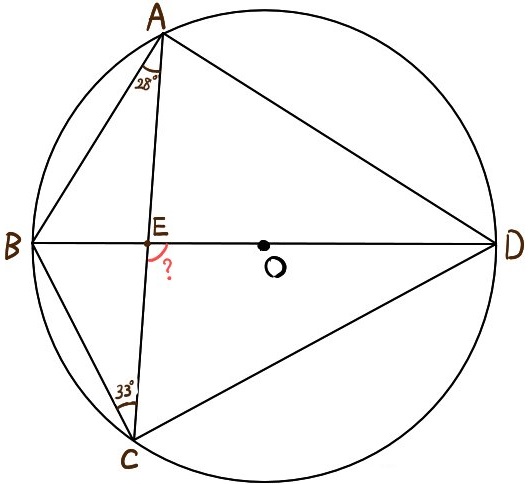



円や半円の問題 円周角と中心角の難問 中学数学 高校入試 坂田先生のブログ



円周角の定理の逆の証明



2



2



円周角の定理とは 定理の逆や証明をわかりやすく解説 受験辞典



2



円周角の定理の逆とは わかりやすく解説 証明問題付き テラコヤプラス By Ameba




円周角の定理の逆 無料で使える中学学習プリント




中学数学 円周角の定理 円周角の定理の逆 Youtube




円周角の定理 作図から証明まで 中3数学 中学生 数学のノート Clearnote




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者



高校入試 英語 数学 円周角の定理



円周角の定理の逆とは わかりやすく解説 証明問題付き テラコヤプラス By Ameba




円周角の定理の逆 数式で独楽する




円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学




動画で学習 2 円周角の定理の逆 数学



円周角の定理とその逆の証明 高校数学マスター



円周角の定理とその逆 Gleamath Com




数学 中3 59 円周角の証明チャレンジ Lv 1 Youtube




円周角の定理の逆の問題です 教えてください Clearnote




円周角の定理の逆をつかった問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく



円周角の定理 証明 逆をスマホで見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ



1



円周角の定理の逆とは わかりやすく解説 証明問題付き テラコヤプラス By Ameba



円周角の定理とは 円周角の定理の証明や問題の解き方を完全解説 Studyplus スタディプラス



接弦定理とは 接線と弦の作る角の定理の証明 覚え方と応用問題 中学 高校 Curlpingの学びblog



円周角の定理の逆とは わかりやすく解説 証明問題付き テラコヤプラス By Ameba




中学数学 よく出る円と相似の融合問題 Pikuu




円周角の定理の逆 中学3年数学 Youtube




平面図形23 円周角の定理の逆 怜悧玲瓏 高校数学を天空から俯瞰する




1 円周角の説明とシミュレーション
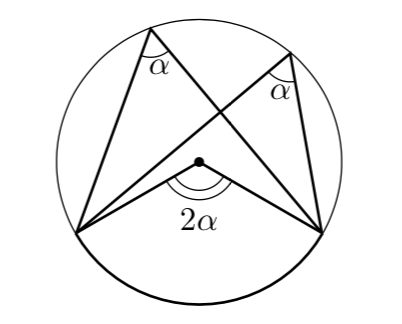



円周角の定理とその逆 Gleamath Com




補助円を使う証明問題 中学3年生の数学より 身勝手な主張




図形の性質 円周角について 日々是鍛錬 ひびこれたんれん
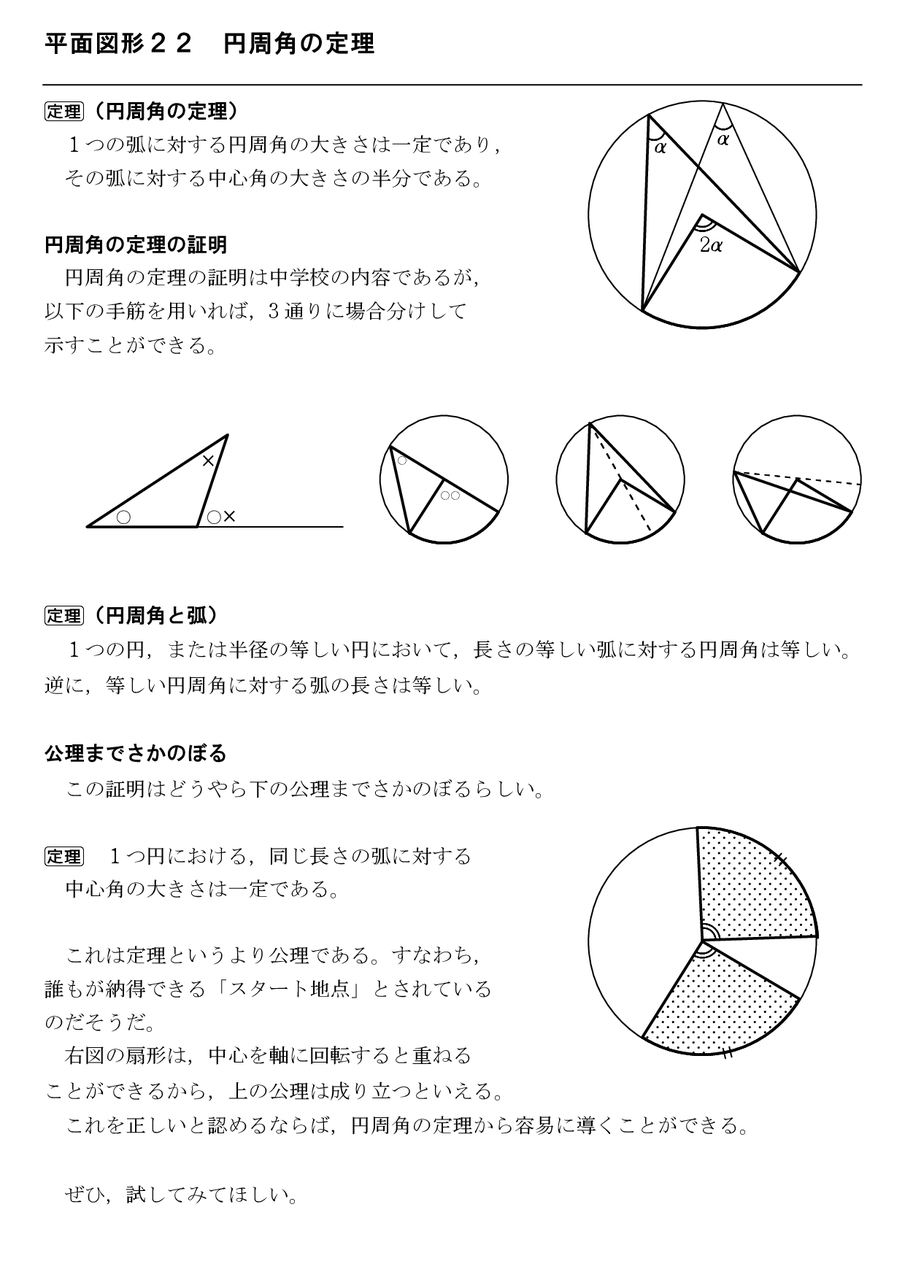



平面図形23 円周角の定理の逆 怜悧玲瓏 高校数学を天空から俯瞰する




中3数学 円の性質7 円周角の定理の逆 すべて無料 星組の中学数学講座
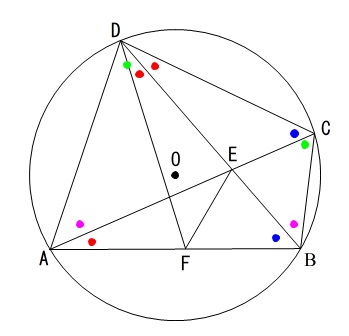



神奈川県公立高校入試18の数学問7 平面図形 の解説
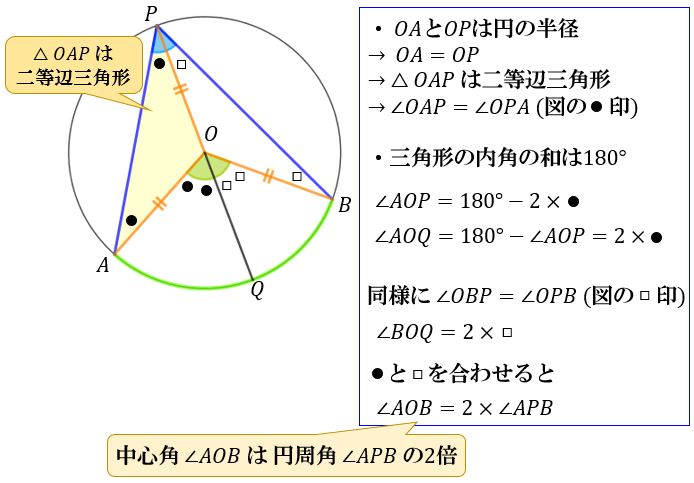



円周角の定理の証明 3つのパターンから分かる円周角と中心角の関係性 アタリマエ



円周角の定理の解説 問題の解き方 数学fun




3分でわかる 円周角の定理の逆の証明 Qikeru 学びを楽しくわかりやすく



Tossランド 円周角の定理の逆




接弦定理まとめ 証明 逆の証明 理系ラボ




中3数学 円周角の定理の逆 の重要ポイント 映像授業のtry It トライイット




写真の問題が分かりません 円周角の定理の逆を使います お願いします Clearnote



Top




中3数学 円周角の定理の逆 の重要ポイント 映像授業のtry It トライイット



円周角の定理とその逆の証明 高校数学マスター




至急質問 中3円周角の定理の逆 至急質問です 中3円周角の定理の逆 右 Okwave



円周角の定理の逆の性質とその証明について



円周角の定理とその逆 思考力を鍛える数学



円




中3数学 円の性質8 円周角の定理の逆 4点が同じ円周上にあることの証明 すべて無料 星組の中学数学講座



1




中学数学 円周角 中心角



1
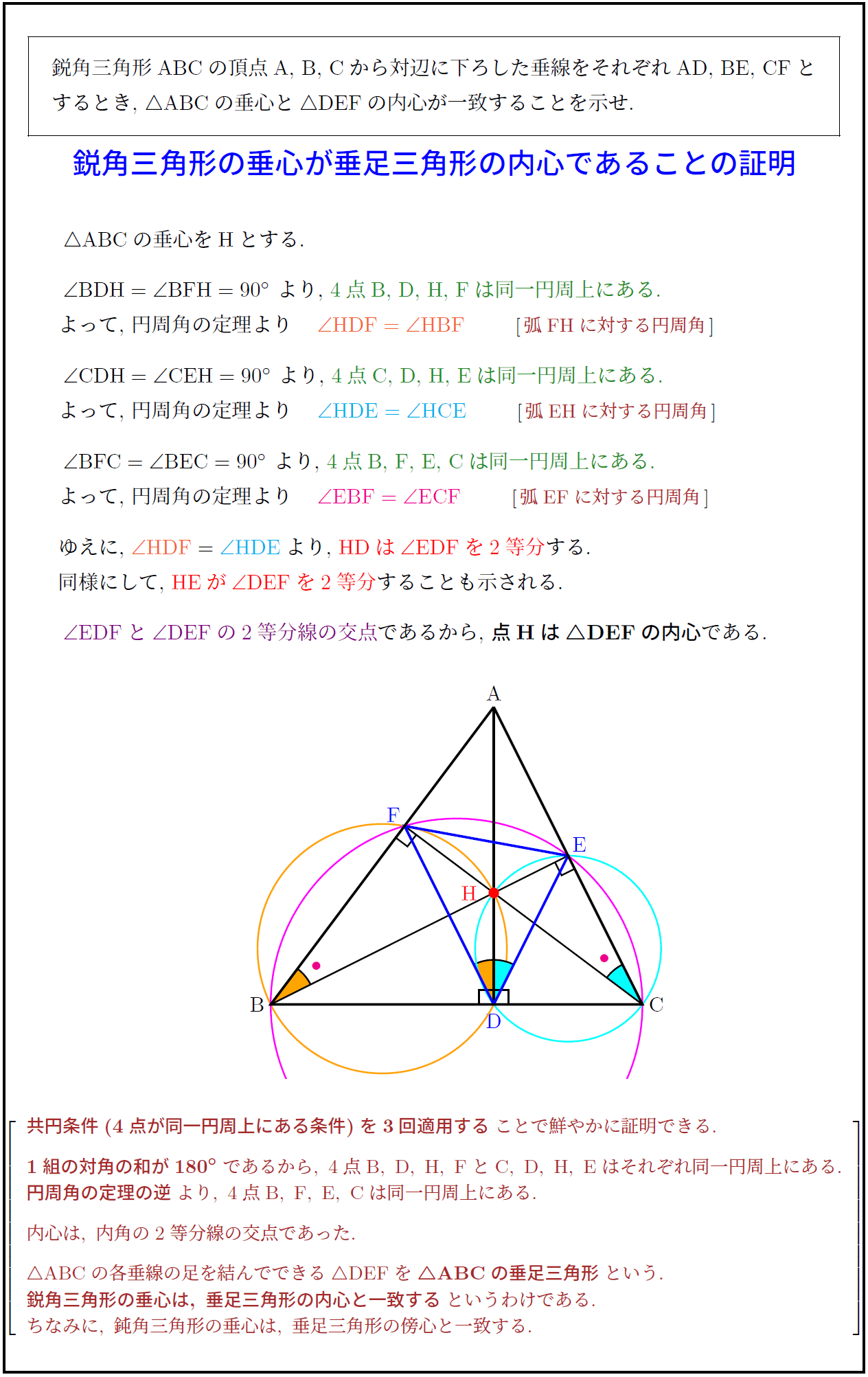



高校数学a 鋭角三角形の垂心が垂足三角形の内心であることの証明 受験の月




円周角の定理の逆をつかった問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく




円周角の定理の逆 身勝手な主張



6章 円 タカラゼミ



円周角の定理の証明を3つ紹介 逆も把握しよう ヒデオの情報管理部屋all Rights Reserved



中3数学 パターン確認 円周角と相似 個別指導塾のyou 学舎日記 公式ブログ




勉強しよう数学解答集 複素数平面の計算で円周角の定理を導く計算方法



図形の性質 円周角について 日々是鍛錬 ひびこれたんれん



1



円周角の定理の逆の証明についてです 画像にある円周角の定理の逆の証明 Yahoo 知恵袋



円周角の定理とその逆の証明 高校数学マスター
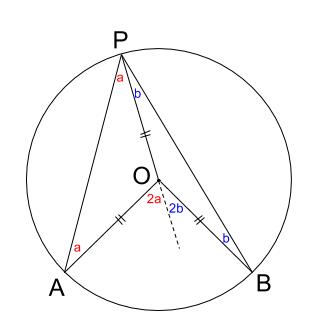



中学数学 円周角の定理はなぜ成り立つのか 中学数学の無料オンライン学習サイトchu Su




円周角の定理 Ict教材eboard イーボード




平面図形14 円周角の定理の逆 怜悧玲瓏 高校数学を天空から俯瞰する



円周角の定理 Twitter Search Twitter




円周角の定理とは 必ず押さえたい7つのポイント 遊ぶ数学



円周角の定理とその逆 思考力を鍛える数学
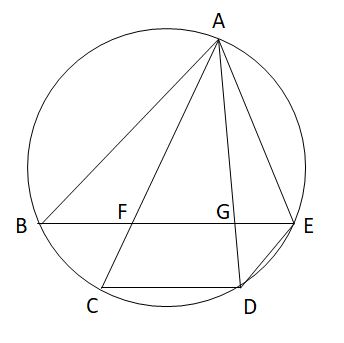



中3数学 円周角の定理を使った証明の定期テスト過去問分析問題 ダイスト




方べきの定理まとめ 証明 逆の証明 理系ラボ
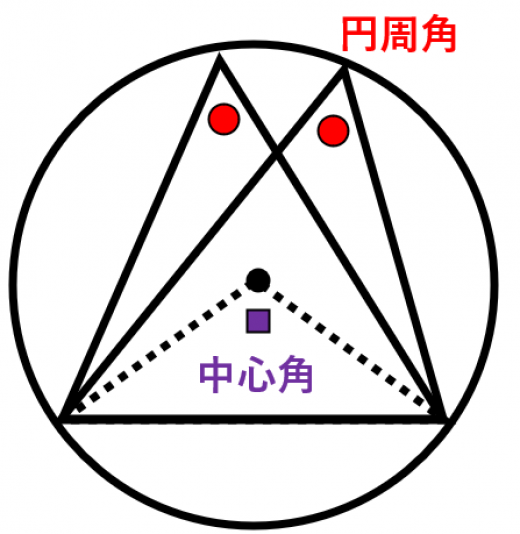



円周角の定理とその逆の証明 高校数学の美しい物語




円周角の定理はこれで完璧 定理の証明と様々な問題の解法



円周角の定理の逆 ノート ひまわり数学教室
コメント
コメントを投稿