200以上 回転移動 書き方 中1 266473-回転移動 書き方 中1

扇形や円の問題と図形の回転移動 駒澤塾 中学受験の算数 理科
Tap to unmute If playback doesn't begin shortly, try restarting your device 映像授業 Try IT(トライイット) SUBSCRIBE You're signed out Videos you watch may be added to the TV's 中1第45回平行移動と回転移動の解答解説はこちらから印刷できます。 → 中1第45回平行移動と回転移動(解答解説) 中1第45回平行移動と回転移動の授業映像は下をクリックしてご覧ください。 中1「1から学ぶ高校受験数学シリーズ」
回転移動 書き方 中1
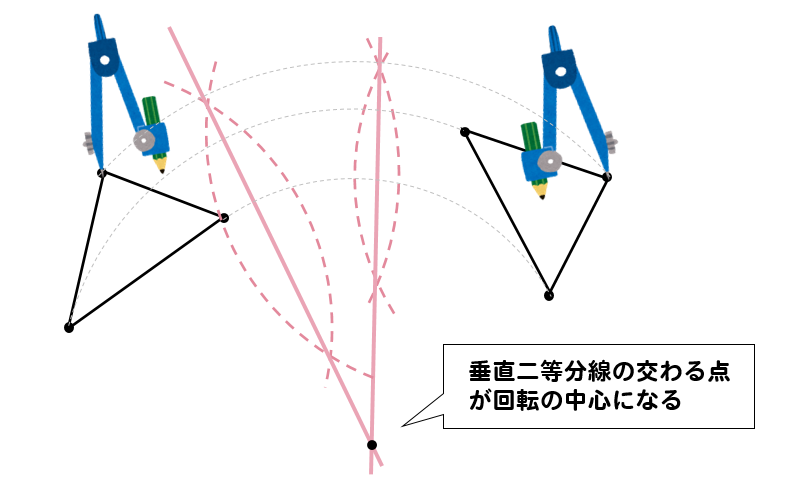
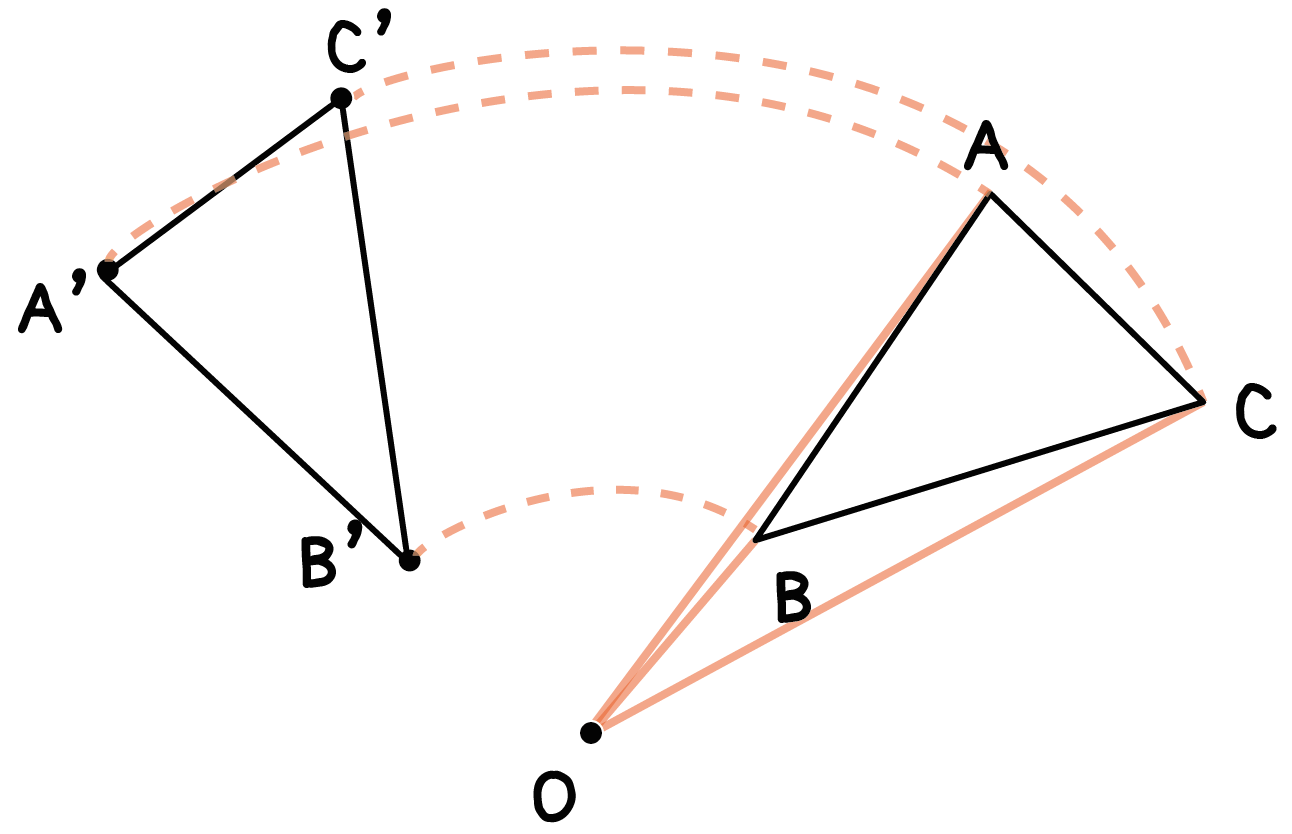
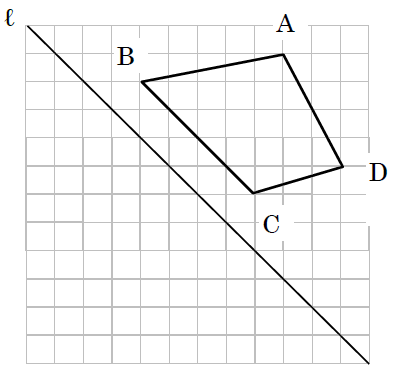
回転移動 書き方 中1- コンパスの針をOに差し,OPの長さを開き, 回転させたい方向に弧をかく。 (3)同様に,他の頂点からもOを中心に 回転させたい方向に弧をかく。 (4)Pの移動先P'を決め,PP'の長さをコンパスでとる。 (5) (3)でかいた「P以外の頂点からの弧」に, コンパスでPP'の長さを写し取る。 これで他の頂点の移動先も決まる。 (6)移動した頂点を結ぶ A平行線のかきかた (1 ここで注目すべきなのは、 回転移動をしても、点 O からの距離は変わらない 、ということです。 つまり、 OA = OD O A = O D などが成り立つということです。 2点からの距離が等しいことから、点 O は、線分 AD の垂直二等分線上にあることがわかります(参考: 基本垂線二等分線の作図 )。 このため、線分 AD, BE, CF の垂直二等分線をかいて、その交点を O

中1数学 篠津中定期テスト対策 100 回転する図形の作図 ブログ アビット
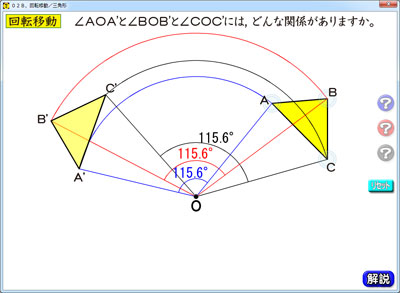
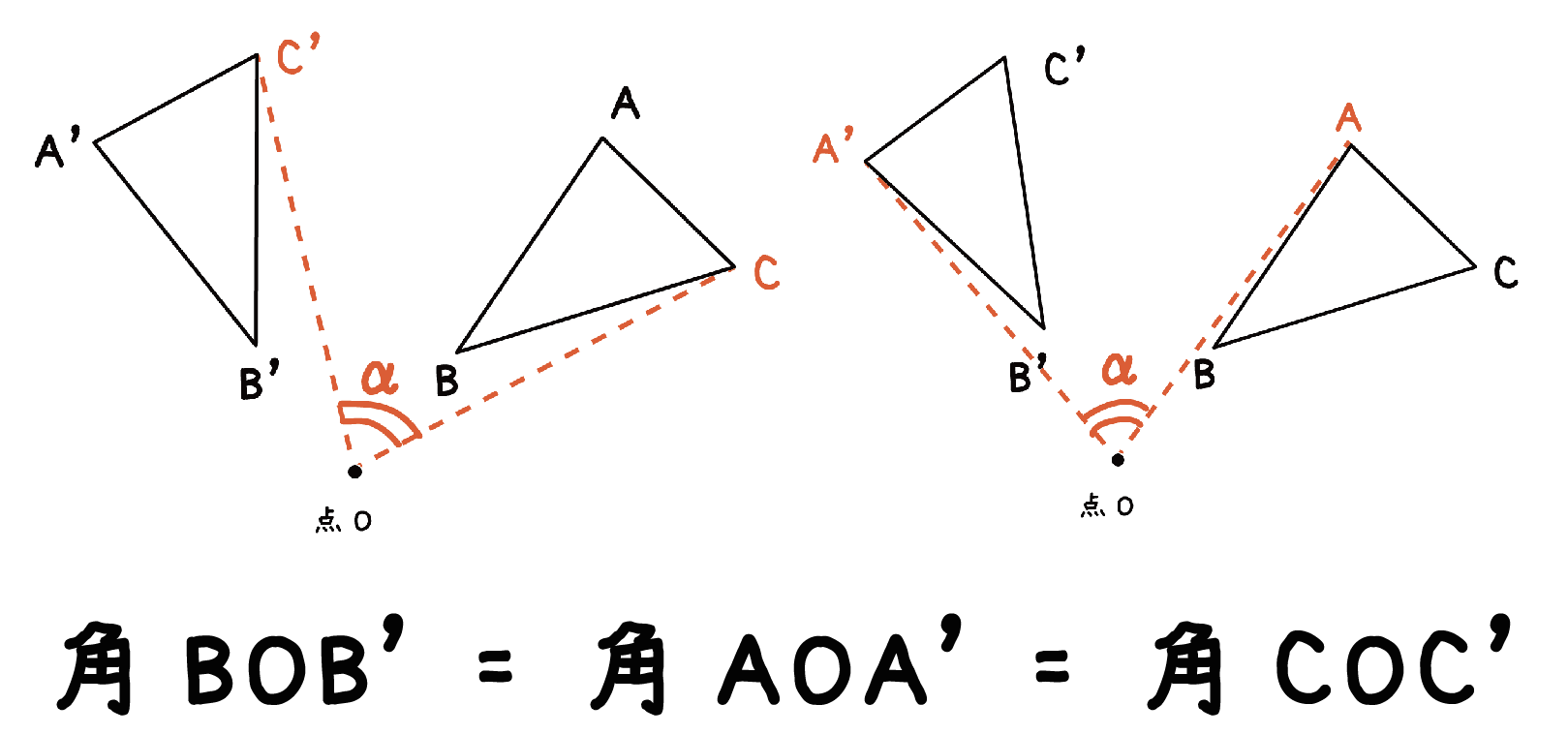
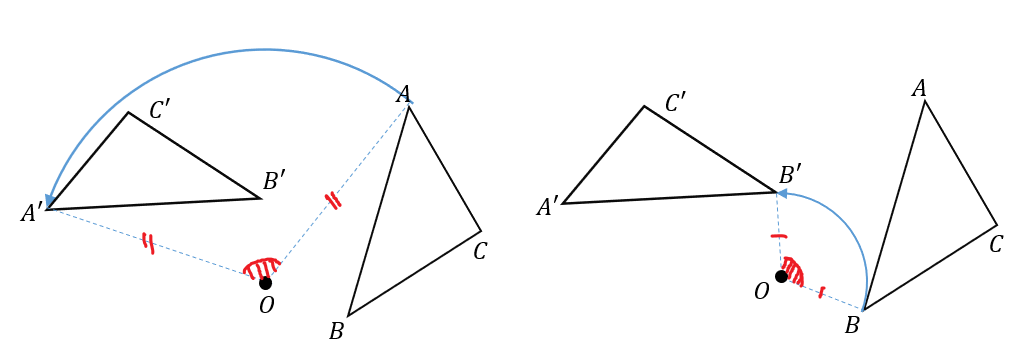
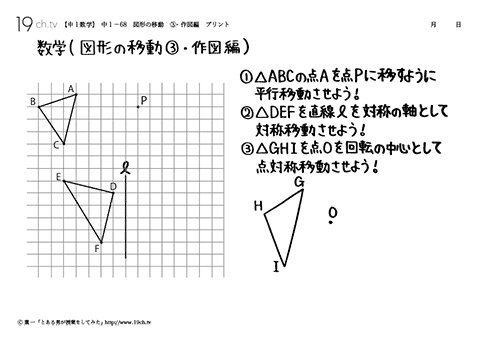
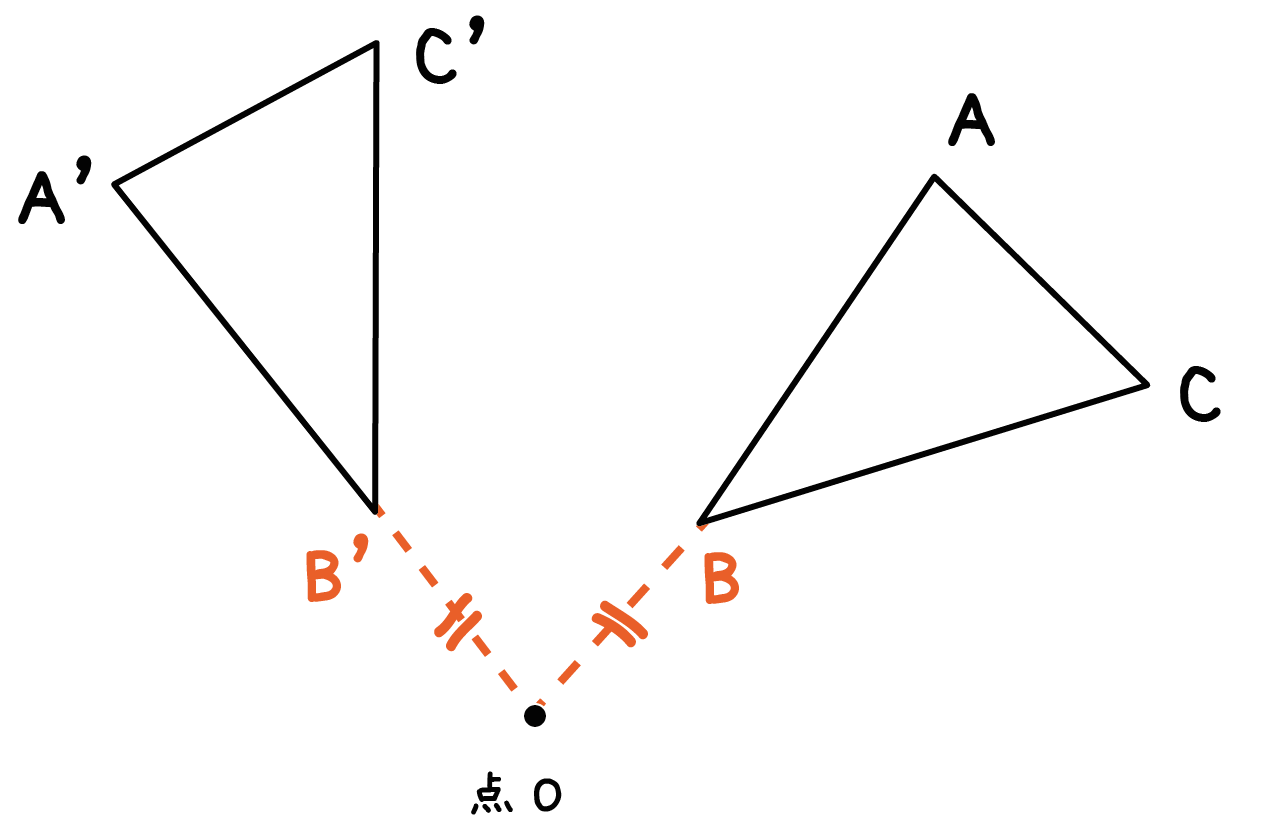
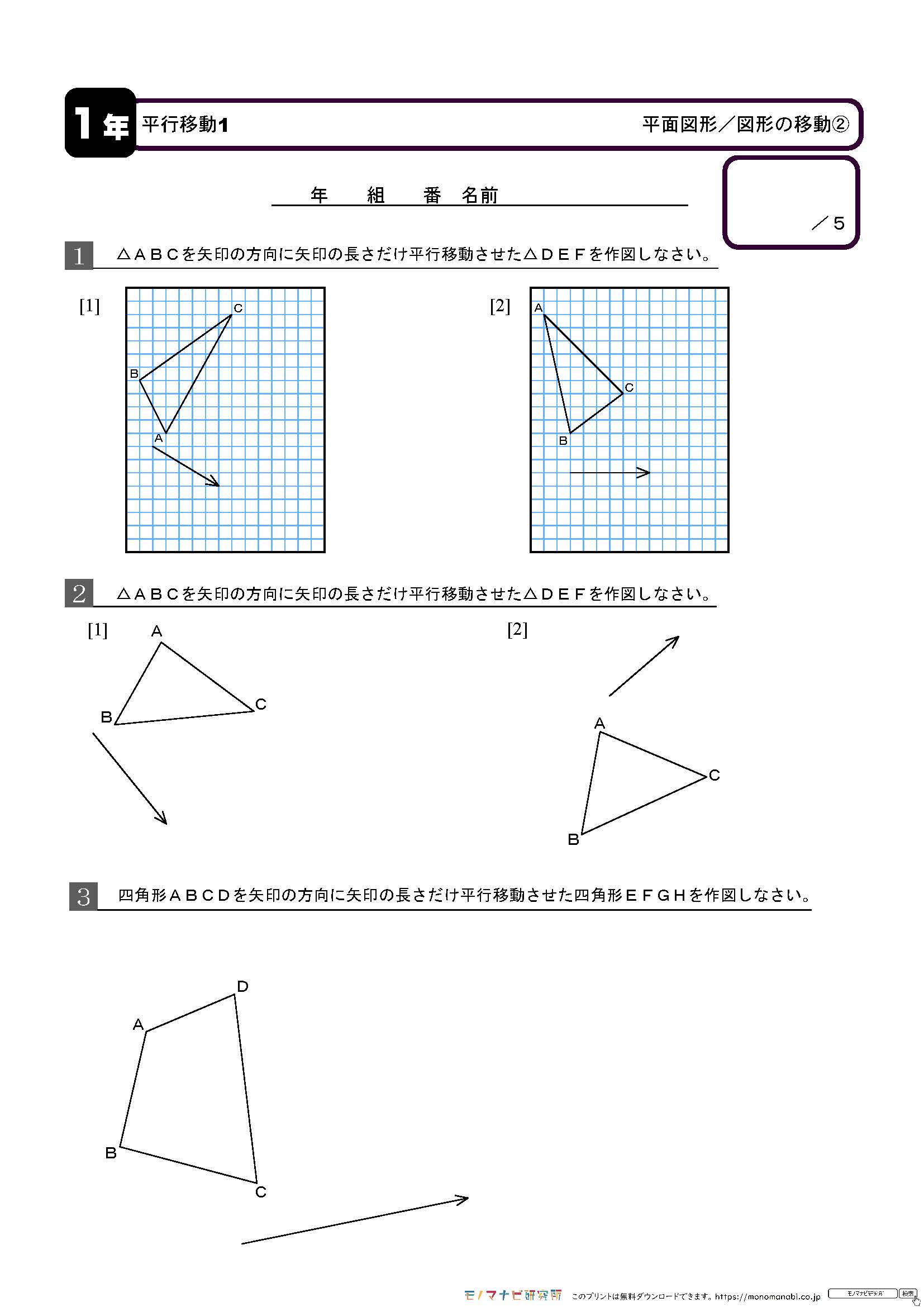
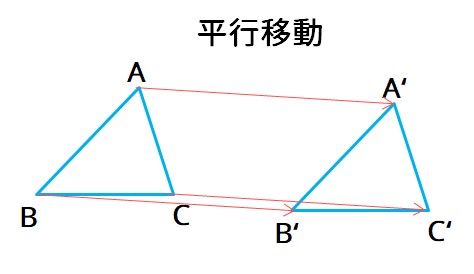
ポイントは図形の点に着目して、すべての点を平行かつ同じ長さで移動させることです。 以上、図形の平行移動の解説でした。 ちなみに回転移動・対称移動の解説についてはこちら。 図形の回転移動の作図手順と性質 中学校1年生の数学では「図形の移動」について習います。 図形の移動は主に「平行移動」「回転移動」「対称移動」の3種類がありますが、今回 回転移動 平面上で、図形を1つの点Oを中心として、一定の角度だけまわして、その図形を移す 例) ABCを点Oを中心に A'B'C'に90°回転移動 作図のやり方 点Oと一番近い点Cを結ぶ Oを中心に半径OCの半円を コンパス を使ってかく OCと弧の90°の角度上に点C'を書く 同様の手順を他 回転移動の中でも、回転角度を180°回転させた時は特別、こんな呼び方をするんだ。 点対称移動 180°の回転移動を行なうこと 180°の回転移動した場合が下の図のようになるんだね。 これを点対称移動と言って、点を対称に移動したってことになるんだね。
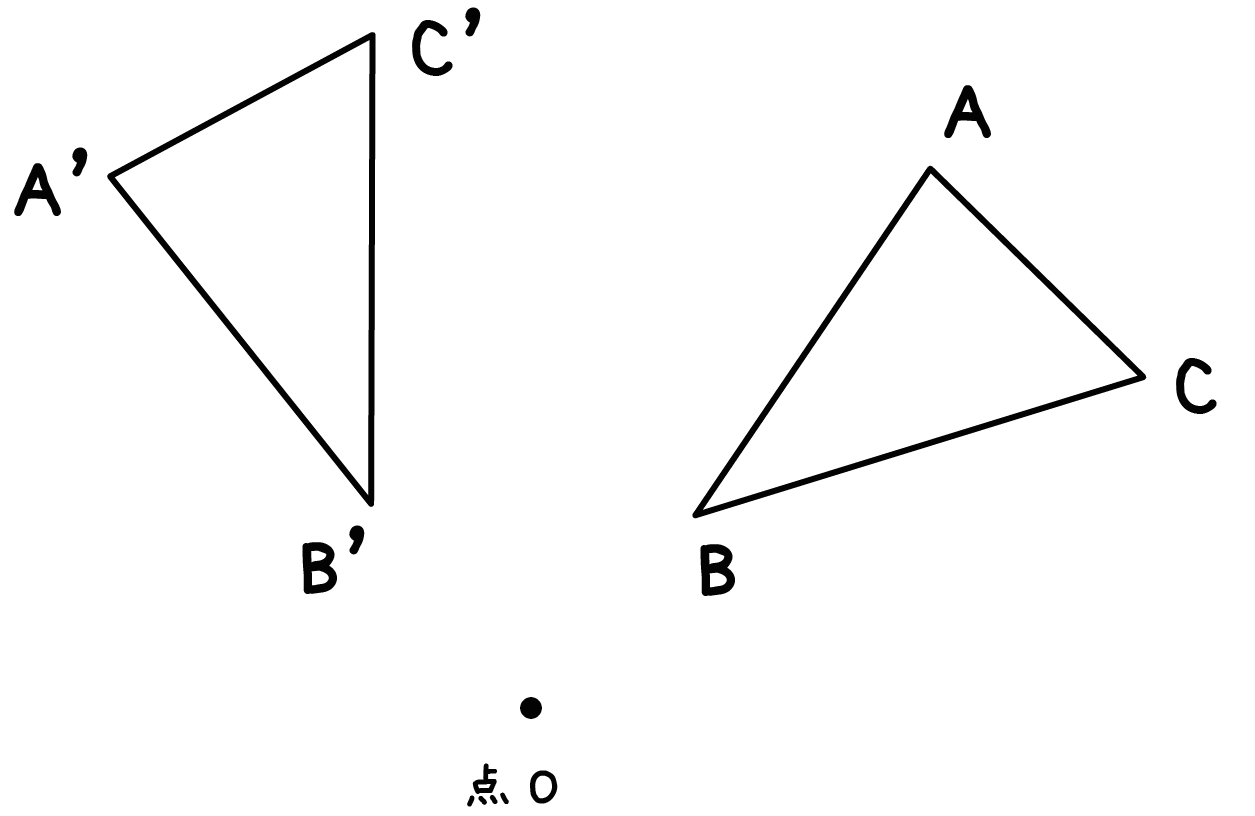
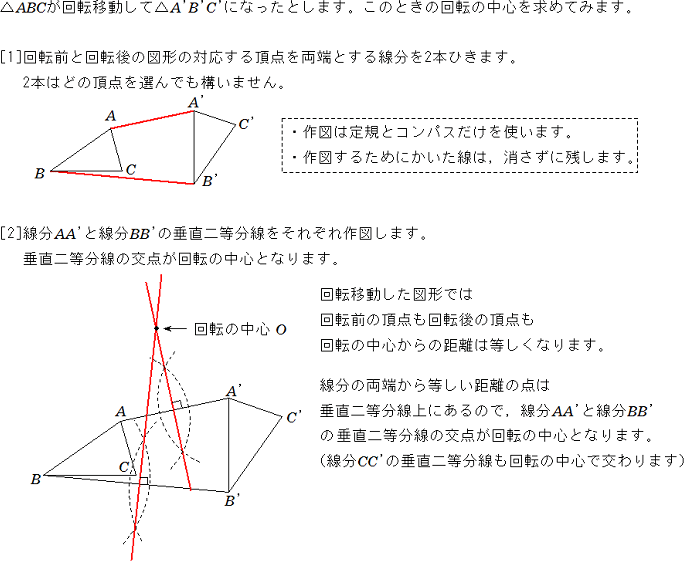
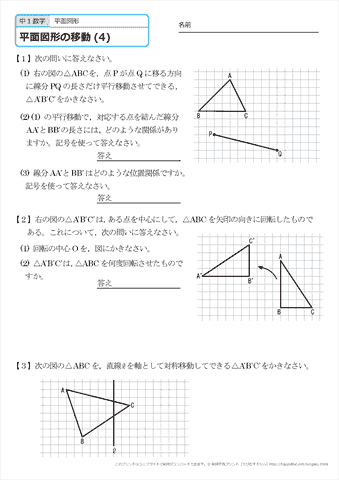
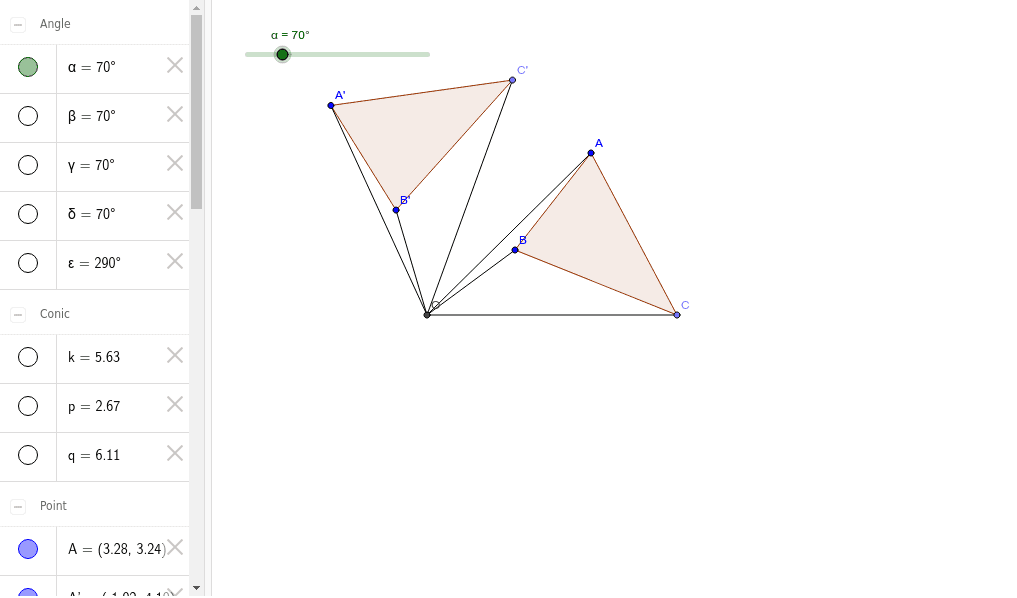
どうやって1本の直定規だけで30 ケーキの9等分 4 回転移動 5 らせん階段の手すりの長さ 6 円の中心点のもとめかた 7 コンパスを使わずに直径100cm程 8 円周率が無理数な理由 9 一つのものを正確に三等分って 10 計算問題2mの紐を三等分にした 11作図の方法を解説! 今回は回転移動の中心を求める作図について考えていこう! 回転移動とは、こんな感じでしたね。 ある点を中心として、図形をぐるっと回転させる移動のこと。 次の図形はある点を中心として回転移動したものです。 その中心となる点を作図しなさい。 どのように回転移動の中心を求めれば良いのでしょうか? 回転移動の特徴を押さえ1) 三角形ABCを移動して三角形A'B'C'になるとき, 線分の長さについてつねにAA'=BB'=CC'が成り立つ。 平行移動 対称移動 回転移動 点対称移動 2) 回転の中心となる点がある。 平行移動 対称移動 回転移動 点対称移動 3)
回転移動 書き方 中1のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 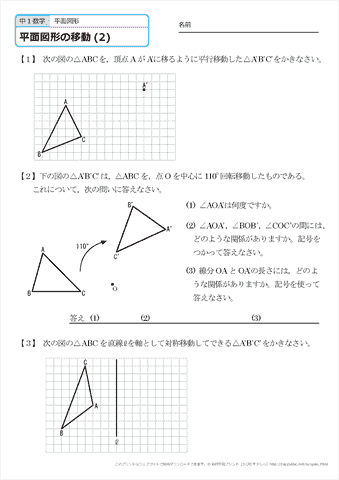 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |  作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |
 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 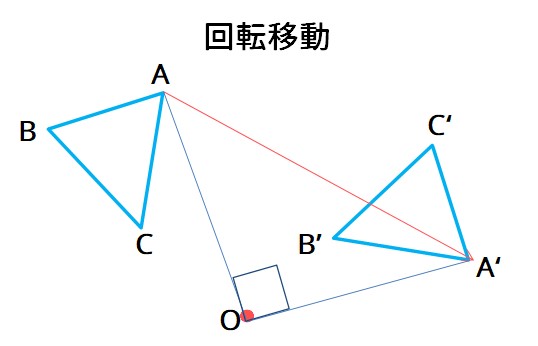 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |
作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |  作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |  作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |
 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 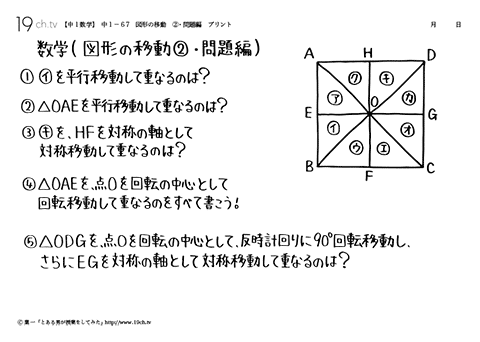 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |
 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |  作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 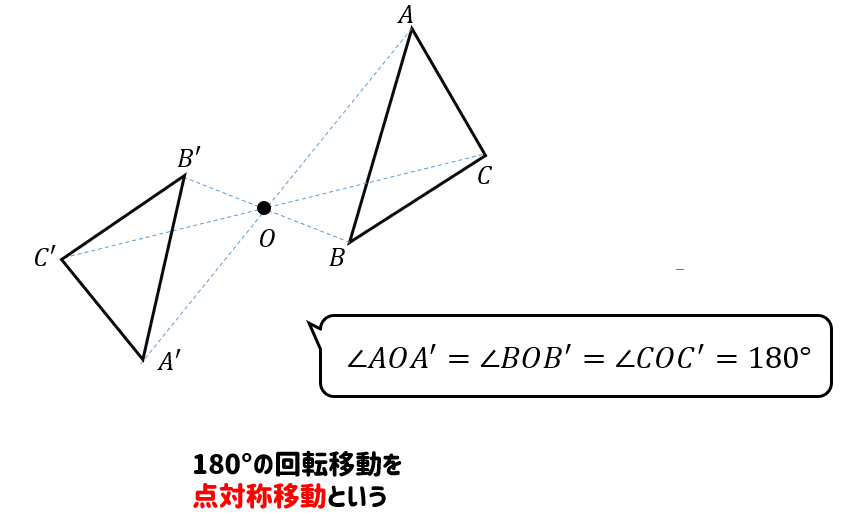 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |
作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |  作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |
 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 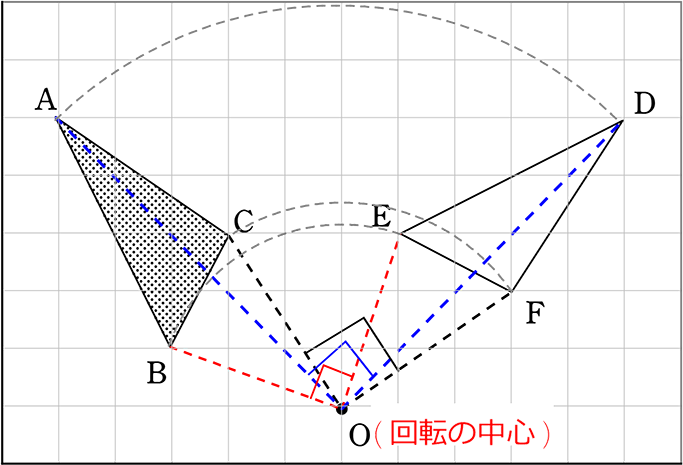 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 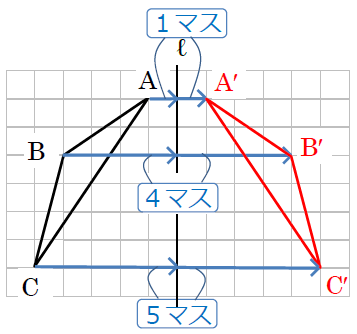 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |
 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |  作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |  作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |
 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 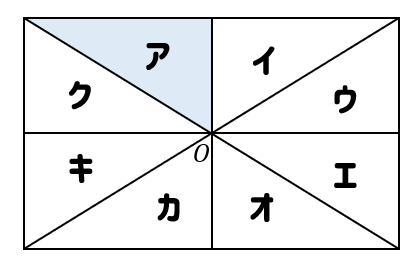 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 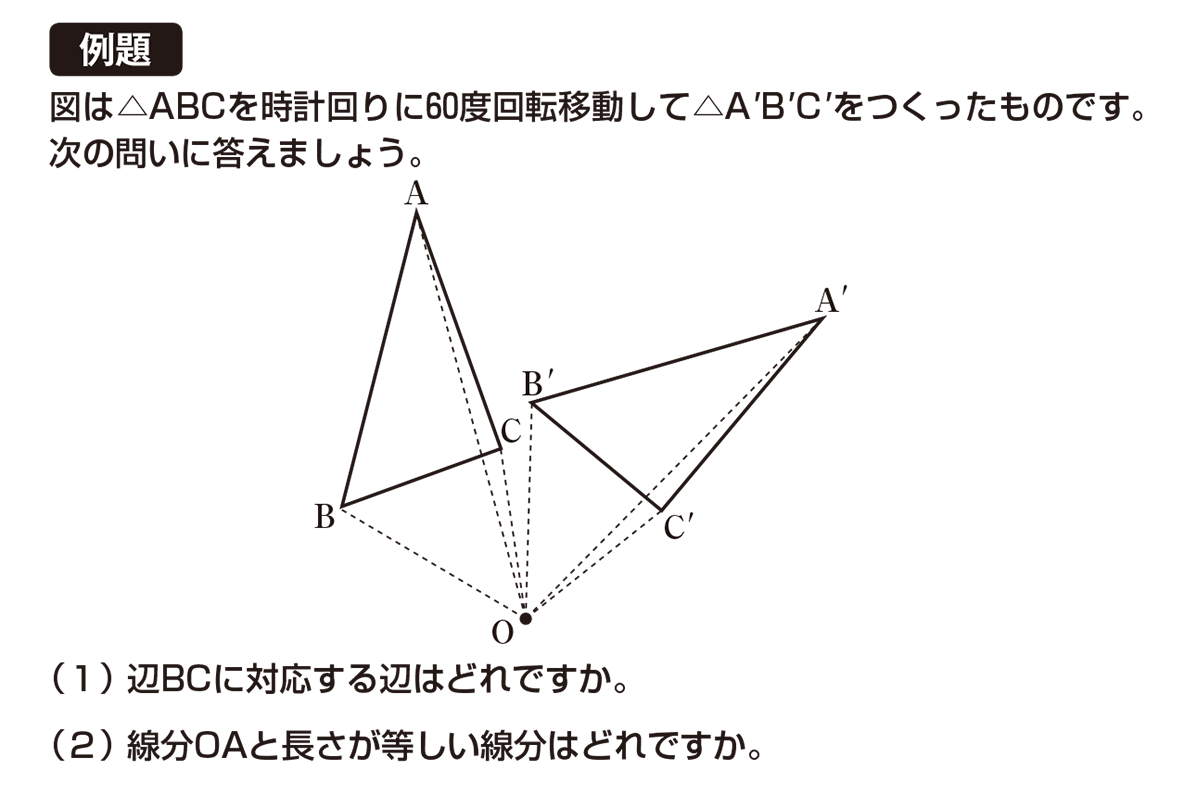 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |
 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 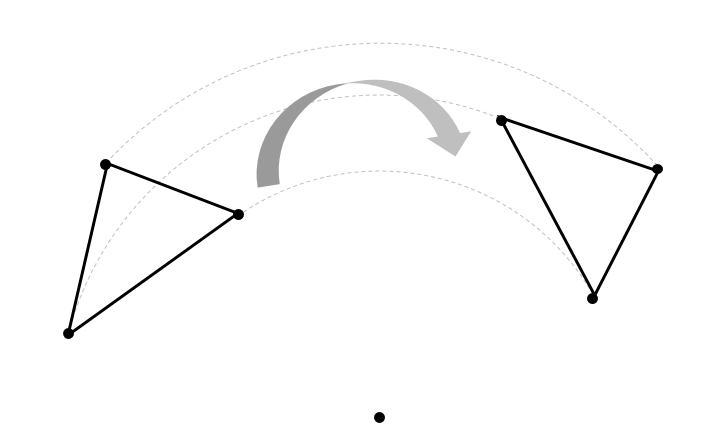 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |
 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 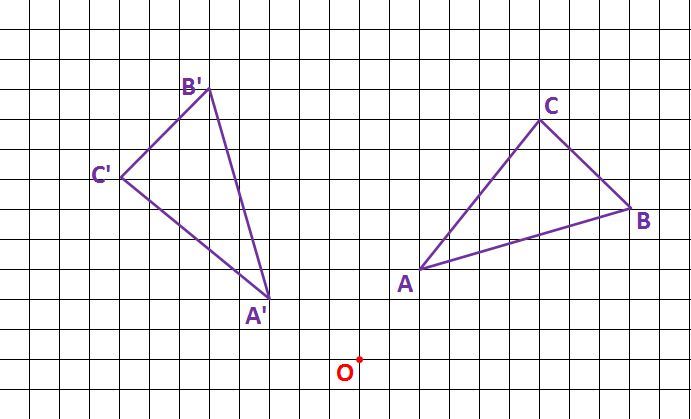 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |
 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |  作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |
 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |  作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |  作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |
 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 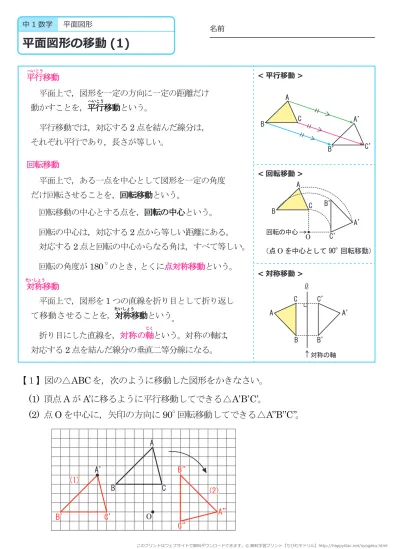 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |  作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |
 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 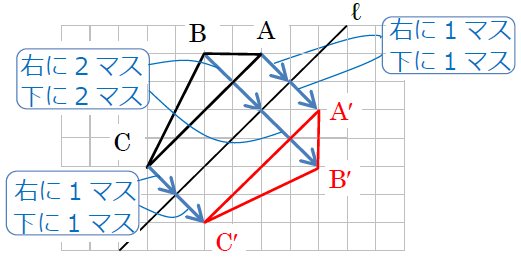 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 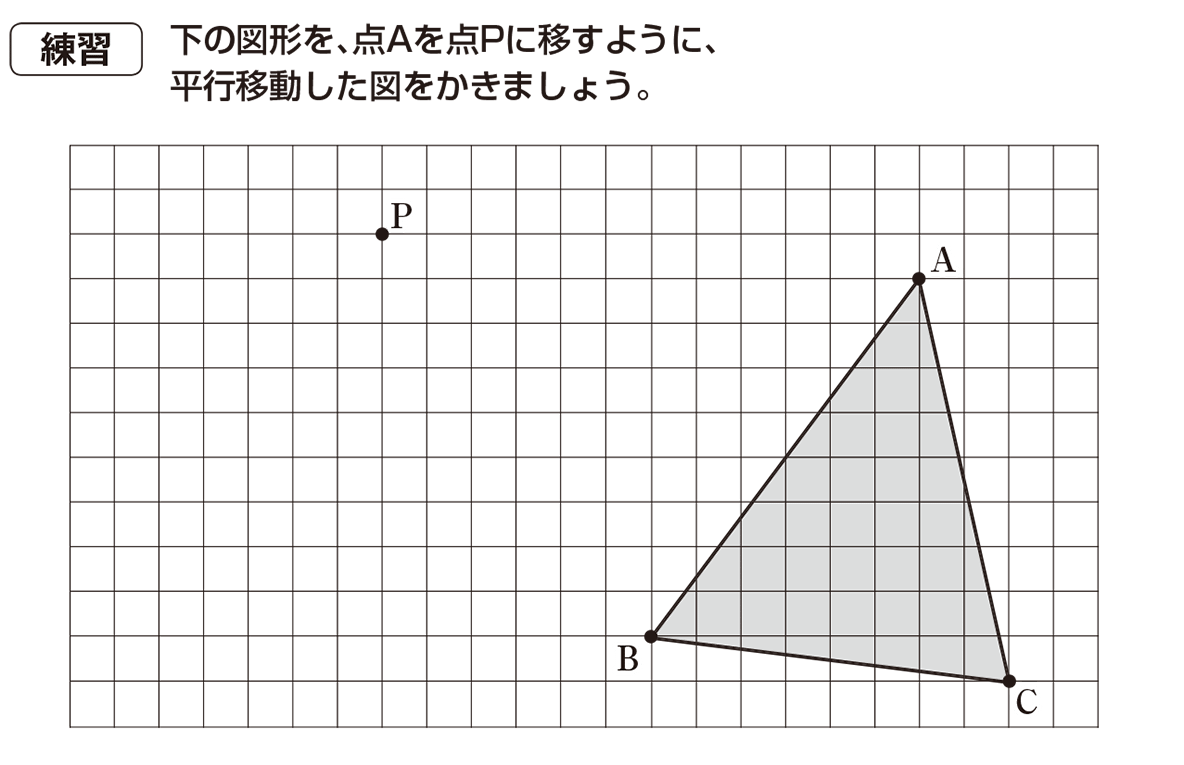 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |
 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |  作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |  作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |
 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |  作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |  作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |
 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |  作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 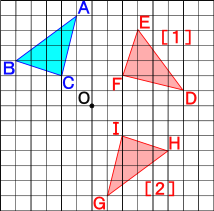 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |
 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |  作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |  作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |
作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 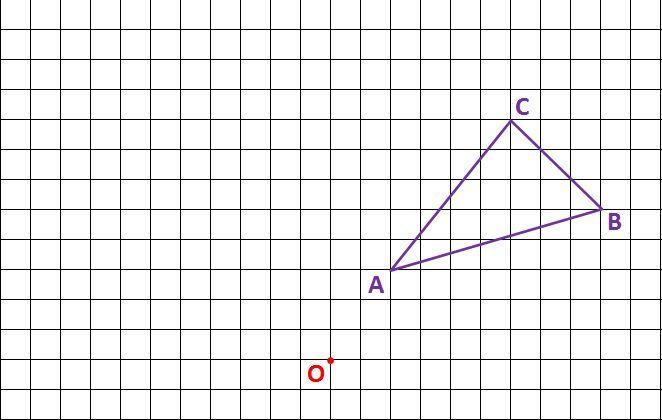 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 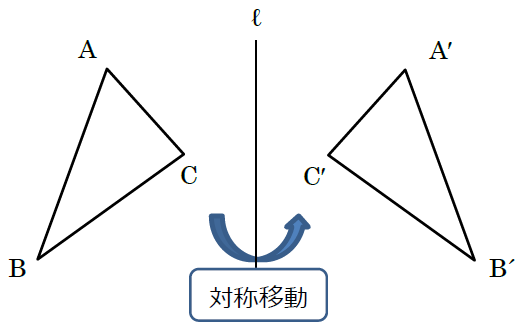 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |
 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 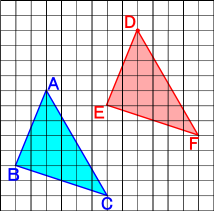 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |
 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 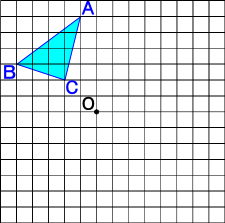 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |  作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |
 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 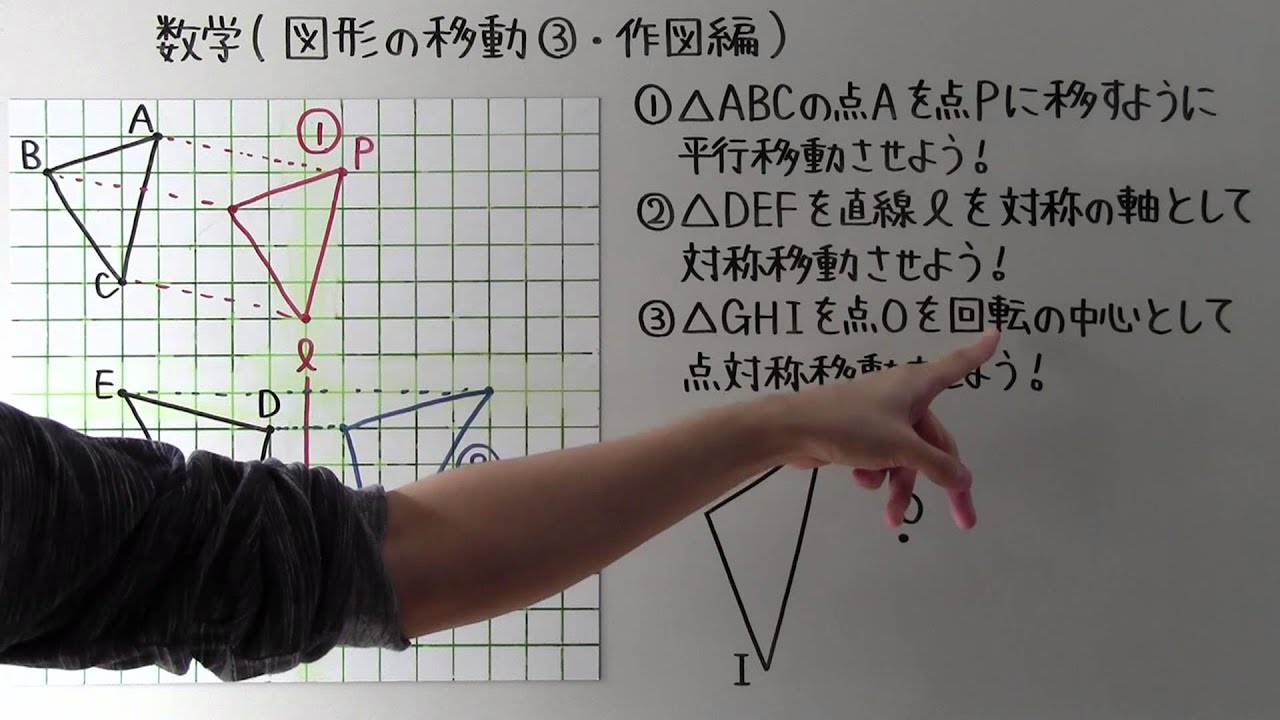 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |  作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |
 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |  作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 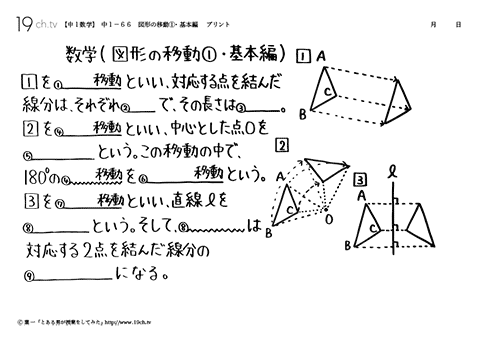 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |
 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |  作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |
 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |  作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 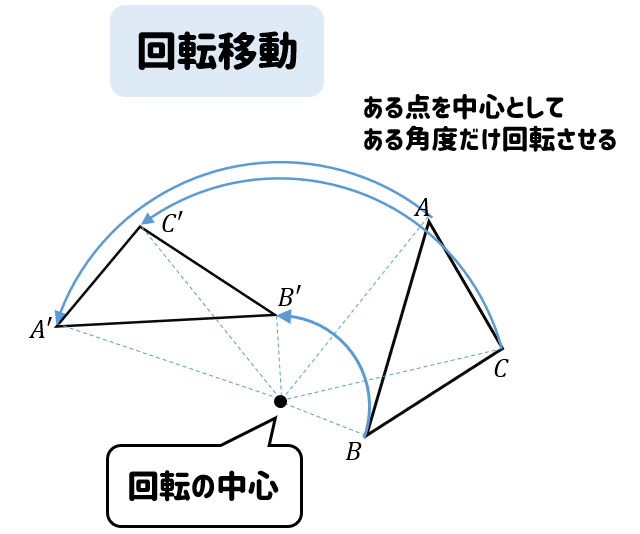 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |
 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 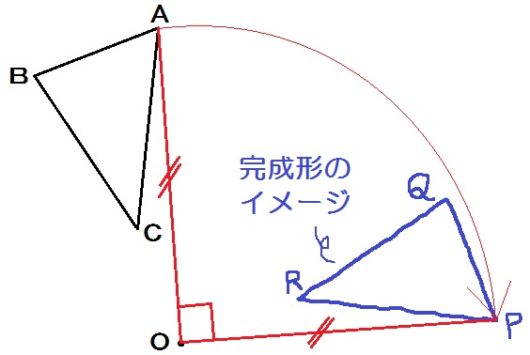 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |
 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 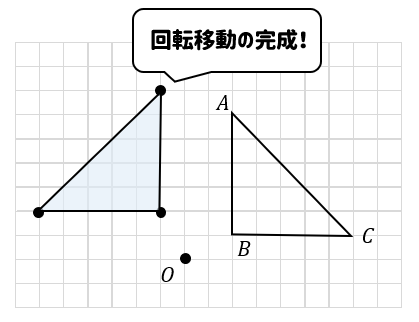 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 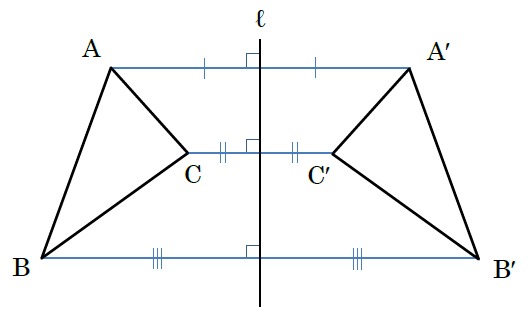 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |
 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 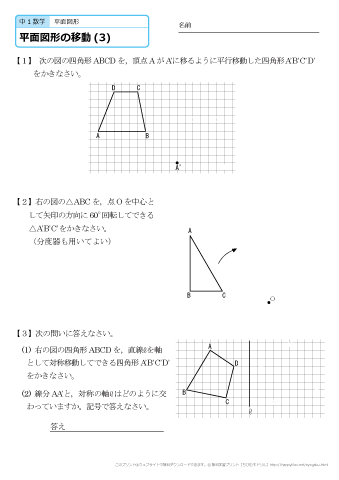 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 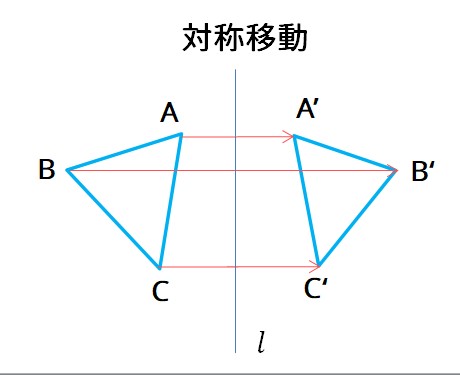 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |
作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 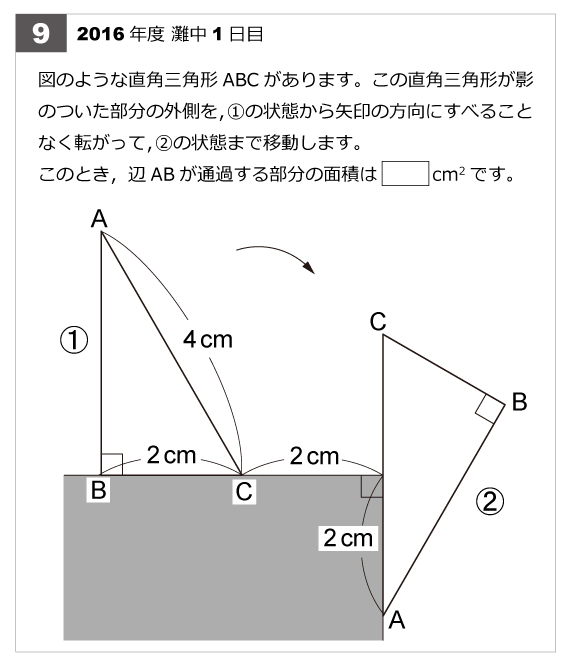 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |
 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |  作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 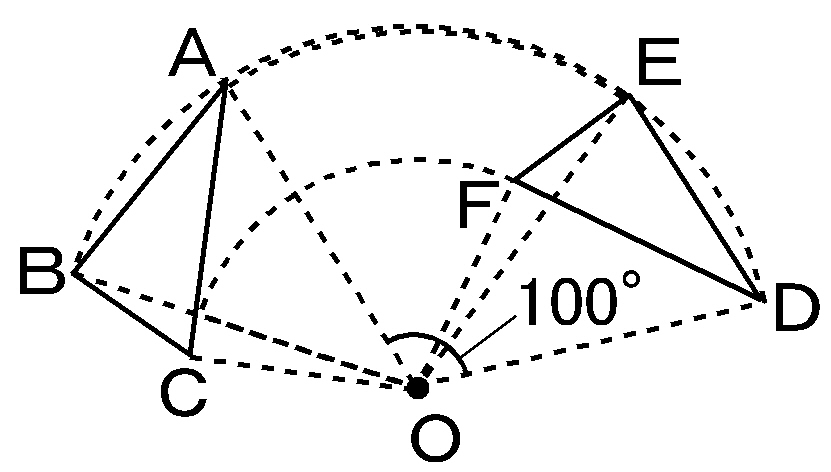 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |
 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 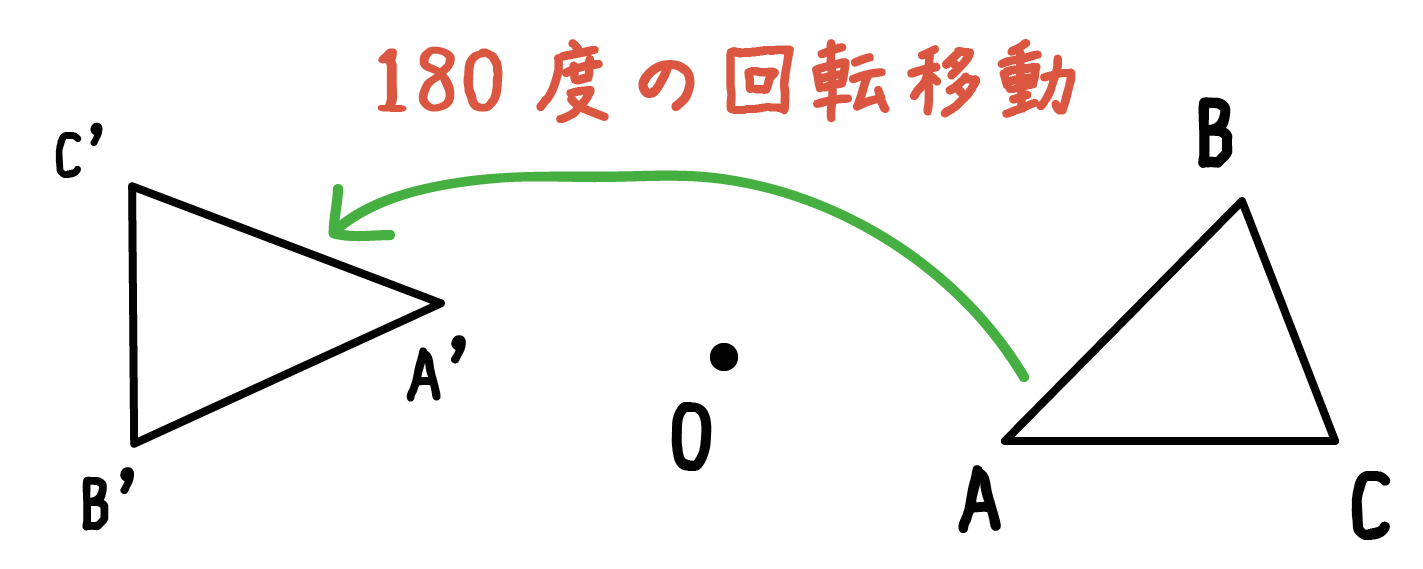 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |
 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |  作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |  作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |
 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |  作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |  作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |
 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ | 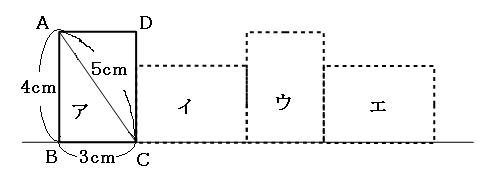 作図 回転移動の中心を求める方法とは 作図の方法を解説 数スタ |
図形の回転移動の作図手順と性質 管理人 1月 29, 19 中学校1年生の数学では「図形の移動」について習います。 図形の移動は主に「 平行移動 」「 回転移動 」「 対称移動 」の3種類がありますが、 今回は回転移動について見ていきましょう。 回転移動とはどういったもので、回転移動した図形にはどういった性質があるのか、また図形の回転移動はどのようにし図形の回転移動の問題の解き方 コツは、移動とともに、図形はどのように動いたのかを頭の中でしっかり想像することです。 点の移動や、図形の平行移動よりは想像しやすいと思います。 回転するので、「円やおうぎ形になるな。
Incoming Term: 回転移動 書き方 中1,
コメント
コメントを投稿